When should the bomb be released for maximum accuracy?

[nameVoid]

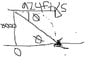
A bomber is flying at an altitude of 25000 feet at a speed of 924 feet per second. When should the bomb be released for it to hit the target. Give your answer in terms of the angle of dpression theta from the plane to the target.

to solve for the time it takes to hit the target
using the equation vtcosTi+[h+vtsinT-gt^2/2]j and taking the distance to the target to be2500/tanT and the initial velocity to be 924/cosT , using the horizontal component and substituting
2500/tanT=924t
t=2500/(924tanT) if the bomb is released at t=0 in terms of theta so the answer would be realease the bomb when t=0?

 

[Raskolnikov]

x = 25000/tan(theta) feet = horizontal distance from initial position and target.

For the horizontal components,
v_i = 924 ft/s
a = 0
Thus, t = x/v_i = 25000/tan(theta)/924.

For the vertical components,
t = same as horizontal component = 25000/tan(theta)/924.
v_i = 0 m/s
a = -32 ft/s^2
y = 25000 ft.

y = v_i*t - .5a*t^2, which plugging in the values gives us

25000 = 0 - (-16)(25000/tan(theta)/924)^2, which simplifies to

tan(theta) = 4*50*sqrt(10) / 924
= 50sqrt(10)/231.

Therefore, theta = tan^-1[50sqrt(10)/231] \approx 34.39^o

To answer the question, I suppose the bomber should release the bomb when the angle of depression is the theta above. I realize this isn't a great measurement of time, but, in my defense, the problem seems to be worded poorly.