fredrogers3 said:
Along the y-direction, -Fg+Fncosθ=ma, a=0
Along the r-direction, Fnsinθ= -m((v^2)/r)
Once again, the book has the above as positive. I get the final answer correctly, with the exception of a negative.
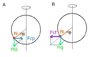
There are a couple of problems in these equations. The most obvious one is that the "r-direction", if we follow the notation in the picture, is not orthogonal with the "y-direction", so there is a component of the weight acting in that direction, too. Plus, the component of the normal force in that direction would be just Fn, not Fn sin θ.
The basic equation is ma = Fn + Fg. In the y-direction: 0 = Fn
y + Fg
y => Fn
y = - Fg
y = mg.
In the x-direction: ma
x = Fn
x + Fg
x = Fn
x.
The acceleration in the x-direction is a
x = -ω
2d, where d is the distance from the axis of rotation. Note the sign is negative, because the acceleration is always opposite to the distance. As can be seen from the picture, d = r sin θ, so a
x = -ω
2 r sin θ.
The tricky part is in computing Fn
x. It seems it should be Fn
x = Fn sin θ. This, however, leads to an unexpected result in the end. Angles can be positive and negative, and the usual convention is that the positive direction is counter-clockwise (thus the angle shown in the picture is in fact negative). Following the usual convention, it can be seen from the picture that for a positive angle, the x-component of Fn should be negative, and positive otherwise. Thus Fn
x = -Fn sin θ and the equation in the x-direction is
-m ω
2r sin θ = -Fn sin θ.