Where are the maximum stresses located in a thin plate with opposing forces?

[ladil]

Hello,

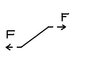
I need some help (or a lot) of calculating where and how much the maximum stress is in a plate as seen in my attached figure.

It´s a thin plate (1mm) that is designed as my picture and it has two forces acting in opposite direction.

How do I calculate where the maximum stresses in the plate would be?

Thank you. Any other dimensions are arbitrary.

 

[Mapes]

An immediate challenge to solving this is that, if the loads are correct, the object is not in static equilibrium. It will start rotating clockwise. So either the position is correct and the loads are incomplete, or one needs to find the equilibrium position.

 

[ladil]

I´m sorry.

The Force applied to the left in the figure can be neglected.
It should be completely constrained in that position.

 

[Mapes]

So you'll have an axial tensile load of magnitude F, along with a bending moment that increases as the lever arm from F increases, reaching its maximum at the wall. Know what I mean?

 

[ladil]

I understand a little bit.
Should I do a equlibrium equation?
F-R=0 in the horisontal direction? R being reaction force on the wall.

I need some more assistance before I can go on.

Thank you.

 

[Mapes]

Exactly; solve the equilibrium equations for horizontal and vertical forces and for moments. At any point, then, you can find the normal stress from \sigma_{11}=F/A-My/I, where y is the distance from the neutral axis and I is the second moment of area. This equation is derived in any Mechanical of Materials textbook.

 

[ladil]

Thank you.