Where Did I Go Wrong with My Hydraulic Car Lift Plot?

[pHysicsN0OB]

My plot didn't come out correctly, so I know I did it wrong. Where did I go wrong or was I even close?

1. Homework Statement
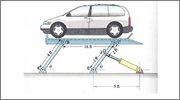
The hydraulic car lift shown in Fig 1 will be used to lift a vehicle of weight W. Determine the force in the hydraulic actuator required support the vehicle as a function of angle θ and the weight of the vehicle, W. Neglect the weight of the components of the lift as they will be negligible with respect to the weight of the vehicle. Assume that the weight of the vehicle is centered between points B and C.

Generate a plot of the ratio of actuator force to vehicle weight (F(actuator)/W) as a function of θ in the range 5 ≤ θ ≤ 60 degrees. If the maximum force the actuator can apply is 24 kip, determine the minimum value of θ that a 4,000 lb vehicle can be lifted from.

The attempt at a solution

 

[Bystander]

sinφ/5 = sinθ/A is good. F/W = cos θ/sinφ is good. What's sinφ?

 

[pHysicsN0OB]

sinφ/5 = sinθ/A is good. F/W = cos θ/sinφ is good. What's sinφ?

I'm suppose to plug all of this into excel and make a plot with a line curving with θ being between 5 ≤ θ ≤ 60 degrees.

My idea was this:
Plug in θ and get A
A^2=2^2+5^2-2(2)(5)cosθ

Then I'll plug in both θ and A to get Phi.
φ=arcsin[(5sin(θ)/A)]

Then I'll plug θ and φ
F/W = cos θ/sinφ

But when I do that on excel, I don't get a curved line. I get more of an up and down line.

This is what I used in the cells with A2:A57 having the numbers 5 through 60.
=sqrt(2^2+5^2-2*2*5*COS(A2*(180/PI())))
=ASIN((5*SIN(A2*(180/PI())))/B2)
=COS(A2)/SIN(C2)

 

[Bystander]

You've already solved for sin(phi) in terms of theta ---

sinφ/5 = sinθ/A is good.

you don't have to go 'round Robin Hood's Barn to get it ---

My idea was this:
Plug in θ and get A
A^2=2^2+5^2-2(2)(5)cosθ

Then I'll plug in both θ and A to get Phi.
φ=arcsin[(5sin(θ)/A)]

Then I'll plug θ and φ
F/W = cos θ/sinφ

(that ain't quite the green of Sherwood Forest, but it'll do) --- forget this --- take what you've already done, substitute for sin(phi), and do the plot --- you'll even know what the shape is supposed to be --- it's a recognizable function.

 

[pHysicsN0OB]

You mean just go directly with F/W = cos θ/sinφ and leave out this...

Plug in θ and get A
A^2=2^2+5^2-2(2)(5)cosθ
Then I'll plug in both θ and A to get Phi.
φ=arcsin[(5sin(θ)/A)]

If so, where would I get phi from if I'm only starting with θ?

 

[Bystander]

Rearrange the first equation, sinφ/5 = sinθ/A to isolate sin(phi) --- plug that into F/W = cos(theta)/sin(phi).

 

[pHysicsN0OB]

Rearrange the first equation, sinφ/5 = sinθ/A to isolate sin(phi) --- plug that into F/W = cos(theta)/sin(phi).

That's what I did.
Rearrange the first equation
A=sqrt(2^2+5^2-2(2)(5)cosθ)

sinφ/5 = sinθ/A to isolate sin(phi)
φ=arcsin[(5sin(θ)/A)]
should there be a parenthesis between 5 and sin?

plug that into F/W = cos(theta)/sin(phi)
F/W = cosθ/sinφ

Unless I'm typing it wrong in excel
A2=5
B2=sqrt(2^2+5^2-2*2*5*COS(A2*(180/PI())))
C2=ASIN((5*SIN(A2*(180/PI())))/B2) should there be a parenthesis between 5 and sin?
D2=COS(A2)/SIN(C2)

 

[Bystander]

sin(phi) = (1/5A) sin(theta); F/W = 5A cot(theta).

 

[(My7H0UgH75)]

I am also stuck on this problem. :( And I am confused why you say that Fcx = 0 for either diagram Fb has an x force and Ex does too. Or maybe I am too tired to think straight.

 

[(My7H0UgH75)]

Did you know that anytime you put something into excel it puts you into radians mode? Opps! I did see that you made that correction for Excel. sorry.

 

[pHysicsN0OB]

sin(phi) = (1/5A) sin(theta); F/W = 5A cot(theta).

I tried 3 ways and I still don't get a good curve.