The expression \(\frac{1}{2}x\) arises when evaluating limits as \(k\) approaches 1, specifically due to the indeterminate form \(0/0\) encountered in the denominator \(2(k-1)\). This situation necessitates the application of L'Hôpital's Rule, which simplifies the limit evaluation process. The limit \(\lim_{t\to0}\frac{\sin(t)}{t}\) is also referenced, yielding a result of 1 when applying L'Hôpital's Rule. The discussion emphasizes the importance of recognizing indeterminate forms in calculus.
PREREQUISITESStudents studying calculus, particularly those focusing on limits and indeterminate forms, as well as educators seeking to clarify these concepts in their teaching.
Yes. The [itex]\ \frac{1}{2}x\[/itex] comes from the fact that the first term has the form 0/0 as k → 1.izen said:Homework Statement
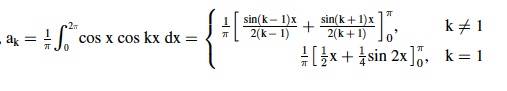
How did [itex]\frac{1}{2}x[/itex] come from at k=1?
Homework Equations
The Attempt at a Solution
because k=1 will make the first term at denominator 2(k-1) = [itex]\frac{0}{0}[/itex]
SammyS said: