Where Does the Ball Become Airborne?

[Matt Raj]

Homework Statement

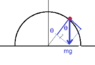
There is an object at the top of a frictionless hemispherical hill with radius R. t time t=0, it is given a small impulse so that it starts sliding down the hill. Find the height from the ground where the ball becomes airborne. Express your answer in terms of R.

Homework Equations

a_c=v^2/r

The Attempt at a Solution

I first attempted setting mv^2/r equal to the force of gravity and the normal force which keep it on its circular path, but I couldn't get a proper equation with it.

 

[BvU]

Hello Matt,

but I couldn't get a proper equation with it.

Well, post what you did get !

 

[mfb]

The centrifugal force and gravity don't point in the same directions. You'll need the components orthogonal to the surface.

Can you find v as function of the height or the angle of the object on the hemisphere?

 

[Matt Raj]

Using the centripetal acceleration, I found that mv^2/R=mg/cos(theta), so v^2=Rg/cos(theta). Furthermore, I used conservation of energy to find that mgR=mgRcos(theta)+1/2(mv^2). I tried solving this system of equations but I got cos^2(theta)-cos^3(theta)=Rg and couldn't go anywhere after that.

 

[timetraveller123]

so v^2=Rg/cos(theta)

i believe this expression is not quite right the height difference between initial position and final position is what you need r/cos theta as far as i can see doesn't represent any height

mv^2/R=mg/cos(theta)

there is also normal force and what can you say about normal force when it just becomes airborne

 

[BvU]

Using the centripetal acceleration, I found that mv^2/R=mg/cos(theta), so v^2=Rg/cos(theta). Furthermore, I used conservation of energy to find that mgR=mgRcos(theta)+1/2(mv^2). I tried solving this system of equations but I got cos^2(theta)-cos^3(theta)=Rg and couldn't go anywhere after that.

Did you make a clear sketch showing what coordinates you use ?

 

[mfb]

Using the centripetal acceleration, I found that mv^2/R=mg/cos(theta), so v^2=Rg/cos(theta). Furthermore, I used conservation of energy to find that mgR=mgRcos(theta)+1/2(mv^2).

Good so far. Something went wrong later because this should lead to a quadratic equation.

Edit: ehild is right, there is a mistake.

 

[ehild]

Using the centripetal acceleration, I found that mv^2/R=mg/cos(theta), so v^2=Rg/cos(theta).

Are you sure?

 

[Matt Raj]

Sorry, I divided by cos(theta) instead of multiplying. The equations should be mv^2/R=mg*cos(theta) and mgR=mgRcos(theta)+1/2(mv^2). Solving this gave me 2/3=cos(theta), so the height that the ball leaves the hill is Rcos(theta)=2R/3.

 

[jbriggs444]

Rcos(theta)=2R/3

You can simplify that further and solve for h, surely?