- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Where is the work done coming from in Helmholtz free energy
- Thread starter tze liu
- Start date
In summary, there is a seeming contradiction in the equation for change in free energy, as keeping temperature and volume constant implies no change in free energy. However, this is resolved by considering the exchange of heat and work with a surrounding medium, where other forms of work besides P-V work can be done. Denbigh's Principles of Chemical Equilibrium provides a more detailed explanation of this concept.
Physics news on Phys.org
- #2
- 8,938
- 2,945
That description is a little confusing, and the Wikipedia article on the topic is no better.
The article goes on to say that [itex]\Delta A[/itex] can be nonzero because the full definition is [itex]dA = -S dt - P dV + \mu dN[/itex], where [itex]N[/itex] is the number of particles, and [itex]\mu[/itex] is the chemical potential. So changing the number of particles can also change [itex]A[/itex]. That's true, but doesn't really address the seeming contradiction, as far as I can see.
But here's the way that I think of the various kinds of "free energy". In the first place, imagine that you have two systems that are thermally isolated (no heat in or out) but share the same volume, as in figure 1:
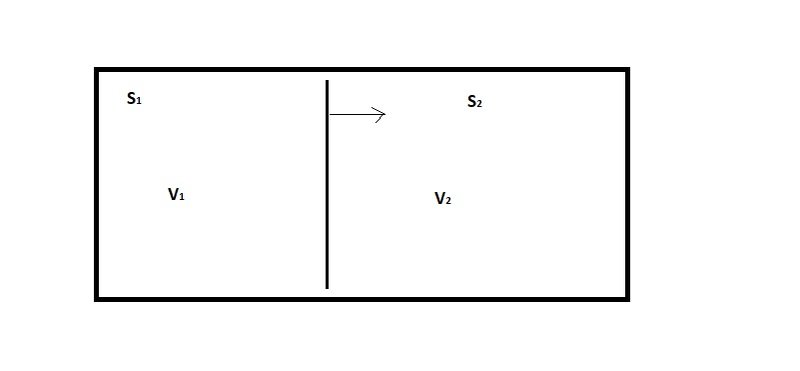
Figure 1: Thermally isolated systems sharing a volume
If system [itex]S_1[/itex] expands by pushing the partition to the right, then it will do work on system [itex]S_2[/itex]. The amount of work done is given by:
[itex]\Delta W = P \Delta V_1[/itex]
We can use the definition of internal energy to relate the work to the heat going in or out:
[itex]\Delta U = \Delta Q - \Delta W = T \Delta S - P \Delta V[/itex]
(Sometimes this is written with a plus sign in front of [itex]\Delta W[/tex], but that depends on whether you're talking about the work done by the system or the work done on the system. If the changes are reversible, as we're assuming, the two are just the negatives of each other).
If the systems are thermally isolated, then [itex]\Delta Q = T \Delta S = 0[/itex], which means that [itex]\Delta W = - \Delta U[/itex]
So the work done by the system is just equal to the loss of internal energy of the system. So in this scenario, the internal energy is a measure of the ability of the system to do work.
Note: The above discussion is for a reversible change. In an irreversible change, the work done by the system can be less than [itex]-\Delta U[/itex]. So we really get:
[itex]\Delta W \leq - \Delta U[/itex]
Now, let's relax the constraint that the two systems are thermally isolated, and instead assume that they are free to exchange heat with a surrounding medium, as in Figure 2:
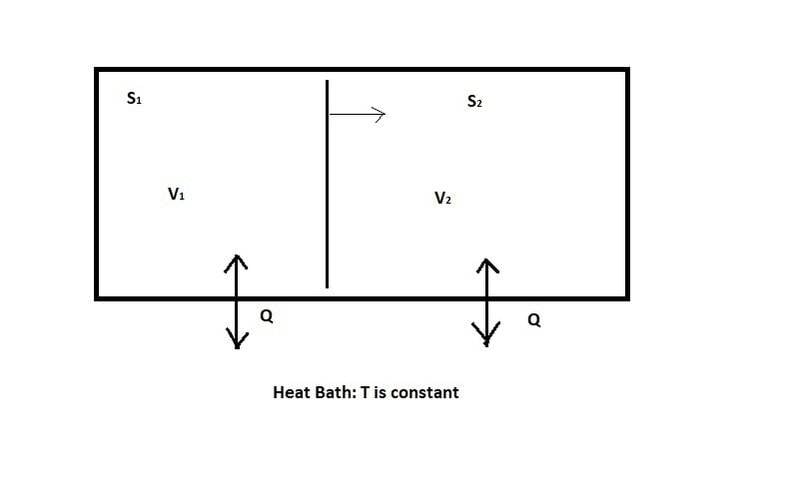
Figure 2: Systems may exchange heat with surrounding medium, but temperature is kept constant
In this case, it's no longer necessarily true that [itex]\Delta Q = 0[/itex] when system 1 expands. As it expands, it can absorb heat from the surrounding heat bath, making [itex]\Delta Q > 0[/itex]. But assuming the heat bath is much larger than either of the two systems, the temperature will remain constant during any reversible change of system 1. So we can use a different thermodynamic identity:
[itex]\Delta A = \Delta U - \Delta (S T) = - P \Delta V - S \Delta T[/itex]
In this case, the heat bath is keeping the temperature constant, so [itex]\Delta T = 0[/itex]. So we have:
[itex]\Delta A = -P \Delta V = -\Delta W[/itex]
So in this case, it is [itex]A[/itex] that gives a measure of the potential of the system to do work, rather than [itex]U[/itex].
Again, this is for a reversible change. For an irreversible change, [itex]-\Delta A[/itex] is an upper bound on the amount of work done by the system:
[itex]\Delta W \leq - \Delta A[/itex]
The discussion in Wikipedia is misleading, because of course, a system can't do any work if the volume is not allowed to change. I think that the issue is resolved by assuming that there is more than one system involved. The volume of the composite system doesn't change, but the volumes of the smaller subsystems can change, and Helmholtz free energy is a measure of the capacity of the subsystem to do work.
We see that the total amount of work that can be extracted in an isothermal process is limited by the free energy decrease, and that increasing the free energy in a reversible process requires work to be done on the system. If no work is extracted from the system then
[itex]\Delta A \leq 0[/itex]
and thus for a system kept at constant temperature and volume and not capable of performing electrical or other non-PV work, the total free energy during a spontaneous change can only decrease.
This result seems to contradict the equation [itex]dA = -S dT - P dV[/itex] as keeping [itex]T[/itex] and [itex]V[/itex] constant seems to imply [itex]dA = 0[/itex] and hence [itex]A = [/itex] constant..
The article goes on to say that [itex]\Delta A[/itex] can be nonzero because the full definition is [itex]dA = -S dt - P dV + \mu dN[/itex], where [itex]N[/itex] is the number of particles, and [itex]\mu[/itex] is the chemical potential. So changing the number of particles can also change [itex]A[/itex]. That's true, but doesn't really address the seeming contradiction, as far as I can see.
But here's the way that I think of the various kinds of "free energy". In the first place, imagine that you have two systems that are thermally isolated (no heat in or out) but share the same volume, as in figure 1:
Figure 1: Thermally isolated systems sharing a volume
If system [itex]S_1[/itex] expands by pushing the partition to the right, then it will do work on system [itex]S_2[/itex]. The amount of work done is given by:
[itex]\Delta W = P \Delta V_1[/itex]
We can use the definition of internal energy to relate the work to the heat going in or out:
[itex]\Delta U = \Delta Q - \Delta W = T \Delta S - P \Delta V[/itex]
(Sometimes this is written with a plus sign in front of [itex]\Delta W[/tex], but that depends on whether you're talking about the work done by the system or the work done on the system. If the changes are reversible, as we're assuming, the two are just the negatives of each other).
If the systems are thermally isolated, then [itex]\Delta Q = T \Delta S = 0[/itex], which means that [itex]\Delta W = - \Delta U[/itex]
So the work done by the system is just equal to the loss of internal energy of the system. So in this scenario, the internal energy is a measure of the ability of the system to do work.
Note: The above discussion is for a reversible change. In an irreversible change, the work done by the system can be less than [itex]-\Delta U[/itex]. So we really get:
[itex]\Delta W \leq - \Delta U[/itex]
Now, let's relax the constraint that the two systems are thermally isolated, and instead assume that they are free to exchange heat with a surrounding medium, as in Figure 2:
Figure 2: Systems may exchange heat with surrounding medium, but temperature is kept constant
In this case, it's no longer necessarily true that [itex]\Delta Q = 0[/itex] when system 1 expands. As it expands, it can absorb heat from the surrounding heat bath, making [itex]\Delta Q > 0[/itex]. But assuming the heat bath is much larger than either of the two systems, the temperature will remain constant during any reversible change of system 1. So we can use a different thermodynamic identity:
[itex]\Delta A = \Delta U - \Delta (S T) = - P \Delta V - S \Delta T[/itex]
In this case, the heat bath is keeping the temperature constant, so [itex]\Delta T = 0[/itex]. So we have:
[itex]\Delta A = -P \Delta V = -\Delta W[/itex]
So in this case, it is [itex]A[/itex] that gives a measure of the potential of the system to do work, rather than [itex]U[/itex].
Again, this is for a reversible change. For an irreversible change, [itex]-\Delta A[/itex] is an upper bound on the amount of work done by the system:
[itex]\Delta W \leq - \Delta A[/itex]
The discussion in Wikipedia is misleading, because of course, a system can't do any work if the volume is not allowed to change. I think that the issue is resolved by assuming that there is more than one system involved. The volume of the composite system doesn't change, but the volumes of the smaller subsystems can change, and Helmholtz free energy is a measure of the capacity of the subsystem to do work.
- #3
tze liu
- 57
- 0
is that your assumption?stevendaryl said:The discussion in Wikipedia is misleading, because of course, a system can't do any work if the volume is not allowed to change. I think that the issue is resolved by assuming that there is more than one system involved. The volume of the composite system doesn't change, but the volumes of the smaller subsystems can change, and Helmholtz free energy is a measure of the capacity of the subsystem to do work.
- #4
- 23,280
- 5,682
You are correct that no P-V work is done. So, if the only focus is P-V work, and the P-V work is zero, then the inequality is satisfied. But there are other kinds of work that can be done on the system (or the system can do on the surroundings), and, if these are operative, then the inequality applies. For a more detailed derivation and description of all this, see Denbigh, Principles of Chemical Equilibrium.tze liu said:Sorry,i want to ask a question here
the note said the volume is "fixed" here.
if the volume if fixed,how comes the work done(because no change of volume) here
i totally get lost here
thank
- #5
tze liu
- 57
- 0
""But there are other kinds of work that can be done on the system""Chestermiller said:You are correct that no P-V work is done. So, if the only focus is P-V work, and the P-V work is zero, then the inequality is satisfied. But there are other kinds of work that can be done on the system (or the system can do on the surroundings), and, if these are operative, then the inequality applies. For a more detailed derivation and description of all this, see Denbigh, Principles of Chemical Equilibrium.
thank
do u means those work done doesn't change the volume of the system?
- #6
- 23,280
- 5,682
Yestze liu said:""But there are other kinds of work that can be done on the system""
thank
do u means those work done doesn't change the volume of the system?
- #7
tze liu
- 57
- 0
when I study thermodynamic,Chestermiller said:Yes
i never heard that the work done doesn't change the volume of the system
So what is such "work done" looks like and how does this "work done" act on the system?
do u have any example?thank
- #8
- 23,280
- 5,682
Electrochemical work, stirring worktze liu said:when I study thermodynamic,
i never heard that the work done doesn't change the volume of the system
So what is such "work done" looks like and how does this "work done" act on the system?
do u have any example?thank
- #9
tze liu
- 57
- 0
why those work doesn't change the volume?Chestermiller said:Electrochemical work, stirring work
- #10
- 23,280
- 5,682
When you stir a liquid in a rigid closed container, does the volume of the container or the liquid change?tze liu said:why those work doesn't change the volume?
- #11
tze liu
- 57
- 0
oh i seeChestermiller said:When you stir a liquid in a rigid closed container, does the volume of the container or the liquid change?
the Work here is the free mechanical work.
but not contributed to the change of volume.
thank
- #12
- 23,280
- 5,682
Don't forget also the possibility of electrochemical work like a battery.tze liu said:oh i see
the Work here is the free mechanical work.
but not contributed to the change of volume.
thank
- #13
tze liu
- 57
- 0
Chestermiller said:Don't forget also the possibility of electrochemical work like a battery.
is this sentense incorrect?Chestermiller said:Don't forget also the possibility of electrochemical work like a battery.
even that the system is thermal isolated and the volume is fixed
there are STILL SOME electrochemical work or other type of mechanical work here
so the delta U is not zero?
Attachments
- #14
- 23,280
- 5,682
You can have a current-carrying wire coming into the container and another wire exiting the container, with the current driven by a battery situated inside the container (elecrochemical). In this case, the internal energy of the system in the container changes (i.e., the battery is running down). The current can drive a motor outside the container. So the system is doing work.tze liu said:is this sentense incorrect?
even that the system is thermal isolated and the volume is fixed
there are STILL SOME electrochemical work or other type of mechanical work here
so the delta U is not zero?
- #15
Lord Jestocost
tze liu said:Sorry,i want to ask a question here
the note said the volume is "fixed" here.
if the volume if fixed,how comes the work done(because no change of volume) here
i totally get lost here
thank
This is always confusing. The essential point is the following:
Calculate the free energy of a system at a given temperature T in state #1: F#1
Calculate the free energy of the system at a given temperature T in state #2: F#2
(to do such calculations you generally need statistical physics)
The work which is done when going from state #1 to #2 in course of a reversible, isothermal process (at temperature T ) is then
Wrev = F#2 - F#1
E.g., in case F#2 < F#1, ABS(F#2 - F#1) is the maximum work you can extract during this isothermal process.
EDIT: In case of irreversible processes you have (work done positive, work extracted negative sign):
ΔW ≥ ΔF
Last edited by a moderator:
- #16
tze liu
- 57
- 0
By the way,Is that true the reverior and the system both are at the same constant temperature in my case?
Chestermiller said:You can have a current-carrying wire coming into the container and another wire exiting the container, with the current driven by a battery situated inside the container (elecrochemical). In this case, the internal energy of the system in the container changes (i.e., the battery is running down). The current can drive a motor outside the container. So the system is doing work.
- #17
- 23,280
- 5,682
No. If you had checked out Denbigh like I suggested, you would have found that T is the temperature of the reservoir and also the temperature of the system at the interface with the reservoir. It is also the initial and final temperature of the system in the initial and final equilibrium states. But, during the process, it is not the temperature of the system (which is non-uniform) except at the interface with the reservoir.tze liu said:By the way,Is that true the reverior and the system both are at the same constant temperature in my case?
Chet
- #18
tze liu
- 57
- 0
however, there is dF=d(U-TS) in my equation.Chestermiller said:No. If you had checked out Denbigh like I suggested, you would have found that T is the temperature of the reservoir and also the temperature of the system at the interface with the reservoir. It is also the initial and final temperature of the system in the initial and final equilibrium states. But, during the process, it is not the temperature of the system (which is non-uniform) except at the interface with the reservoir.
Chet
how can they use the temperature in the reservoir but not using the temperature inside the system?
there are two T in this case
the T in the reservoir and the other T in my system which can be described by F free energy.
why the equation dF=d(U-TS) ignore the temperature change inside the system.
- #19
- 23,280
- 5,682
If the temperature is not uniform within your system during the process, then F (which is a function of equilibrium state) is undefined. If you want to define F within your system when it is not at equilibrium, then you have to integrate the local free energy per unit mass over the mass of your system.tze liu said:however, there is dF=d(U-TS) in my equation.
how can they use the temperature in the reservoir but not using the temperature inside the system?
there are two T in this case
the T in the reservoir and the other T in my system which can be described by F free energy.
why the equation dF=d(U-TS) ignore the temperature change inside the system.
Last edited:
- #20
tze liu
- 57
- 0
it seemsChestermiller said:No. If you had checked out Denbigh like I suggested, you would have found that T is the temperature of the reservoir and also the temperature of the system at the interface with the reservoir. It is also the initial and final temperature of the system in the initial and final equilibrium states. But, during the process, it is not the temperature of the system (which is non-uniform) except at the interface with the reservoir.
Chet
if the temperature is constant in my process, i assume this temperature is T2Chestermiller said:If the temperature is not uniform within your system during the process, then F (which is a function of equilibrium state) is undefined. If you want to define F within your system when it is not at equilibrium, then you have to integrate the local free energy per unit mass over the mass of your system.
and the environment temperature is T1 ( T1 cannot be T2,if so, then there is no heat transfer)
why it should be dF=d(U-T1S) but not dF=d(U-T2S) ?i don't know why they use the environment temperature in the equation but not using the system's temperature( assume the system has constant temperature)
- #21
- 23,280
- 5,682
As I said, see Denbigh.tze liu said:it seems
if the temperature is constant in my process, i assume this temperature is T2
and the environment temperature is T1 ( T1 cannot be T2,if so, then there is no heat transfer)
why it should be dF=d(U-T1S) but not dF=d(U-T2S) ?i don't know why they use the environment temperature in the equation but not using the system's temperature( assume the system has constant temperature)
- #22
- 23,280
- 5,682
Do you really think that, in an irreversible process, the temperature within the system is uniform?
From the Clausius inequality applied to this problem, we have: $$\Delta S=\frac{Q}{T}+\sigma$$ where Q is the heat transferred from the reservoir to the system, T is both the initial and final temperature of the system as well as the temperature of the reservoir (at the heat transfer boundary with the system), and ##\sigma## is the entropy generated within the system during the process (always positive). So we have: $$Q=T\Delta S-T\sigma$$
If we substitute this into the first law of thermodynamics, we obtain:
$$\Delta U=T\Delta S-T\sigma+W$$where W is the work done by the surroundings on the system. From this, it follows that $$W=\Delta F+T\sigma$$Since ##\sigma## is always positive, it follows that $$W\gt \Delta F$$
From the Clausius inequality applied to this problem, we have: $$\Delta S=\frac{Q}{T}+\sigma$$ where Q is the heat transferred from the reservoir to the system, T is both the initial and final temperature of the system as well as the temperature of the reservoir (at the heat transfer boundary with the system), and ##\sigma## is the entropy generated within the system during the process (always positive). So we have: $$Q=T\Delta S-T\sigma$$
If we substitute this into the first law of thermodynamics, we obtain:
$$\Delta U=T\Delta S-T\sigma+W$$where W is the work done by the surroundings on the system. From this, it follows that $$W=\Delta F+T\sigma$$Since ##\sigma## is always positive, it follows that $$W\gt \Delta F$$
Last edited:
- #23
jim mcnamara
Mentor
- 4,770
- 3,816
@tze liu - there is a free to download pdf version of what @Chestermiller referred to.
Hope you can get and read the book.
https://archive.org/details/ThePrinciplesOfChemicalEquilibrium
Chet - FWIW some folks in places outside the US have trouble finding or getting to sources via links - countrywide IP blacklistings, limits on search engines, etc.
Hope you can get and read the book.
https://archive.org/details/ThePrinciplesOfChemicalEquilibrium
Chet - FWIW some folks in places outside the US have trouble finding or getting to sources via links - countrywide IP blacklistings, limits on search engines, etc.
- #24
- 23,280
- 5,682
Here is the direct quote from Denbigh: "Consider the special case (a) that the only heat transferred to the system is from a heat reservoir which remains at the constant temperature T; (b) that the initial and final temperatures, ##T_1## and ##T_2##, of the system are equal, and are equal to the temperature T of the reservoir."
Note that this description fails to mention the important fact that the temperature of the system is not uniform during the process, or that it is equal to T only at the boundary with the reservoir (except in the initial and final states).
Note that this description fails to mention the important fact that the temperature of the system is not uniform during the process, or that it is equal to T only at the boundary with the reservoir (except in the initial and final states).
- #25
tze liu
- 57
- 0
Oh I see.than you very much .There are still problems here.if the temperature at the beginning are equal to the reverior,how comes the heat transfer between them at the beginning?(because it violates the zero law)
- #26
- 23,280
- 5,682
It is only at the boundary that they match. Normal to the boundary, the gas temperature is varying. And the average gas temperature is different from its temperature (and the reservoir temperature) at the boundary.tze liu said:Oh I see.than you very much .There are still problems here.if the temperature at the beginning are equal to the reverior,how comes the heat transfer between them at the beginning?(because it violates the zero law)
- #27
tze liu
- 57
- 0
Chestermiller said:Here is the direct quote from Denbigh: "Consider the special case (a) that the only heat transferred to the system is from a heat reservoir which remains at the constant temperature T; (b) that the initial and final temperatures, ##T_1## and ##T_2##, of the system are equal, and are equal to the temperature T of the reservoir."
Note that this description fails to mention the important fact that the temperature of the system is not uniform during the process, or that it is equal to T only at the boundary with the reservoir (except in the initial and final states).
that means the heat is transfer from the boundary to the gas,and cause the heat transfer from the heat bath to the system boundary?Chestermiller said:It is only at the boundary that they match. Normal to the boundary, the gas temperature is varying. And the average gas temperature is different from its temperature (and the reservoir temperature) at the boundary.
- #28
tze liu
- 57
- 0
tze liu said:Look very strange.are you sure the temperature are equ
that means the heat is transfer from the boundary to the gas,and cause the heat transfer from the heat bath to the system boundary?
thank youjim mcnamara said:@tze liu - there is a free to download pdf version of what @Chestermiller referred to.
Hope you can get and read the book.
https://archive.org/details/ThePrinciplesOfChemicalEquilibrium
Chet - FWIW some folks in places outside the US have trouble finding or getting to sources via links - countrywide IP blacklistings, limits on search engines, etc.
- #29
- 23,280
- 5,682
On the bath side of the boundary, the thermal conductivity of the heat bath liquid is taken to be very large, so that the magnitude of the temperature gradient in the bath liquid is very small, even for a finite heat flux. This is an inherent characteristic of an ideal heat bath. So there can be heat flow in the bath to- and from the boundary even though the temperature gradient is tiny.tze liu said:that means the heat is transfer from the boundary to the gas,and cause the heat transfer from the heat bath to the system boundary?
- #30
tze liu
- 57
- 0
oh i seeChestermiller said:On the bath side of the boundary, the thermal conductivity of the heat bath liquid is taken to be very large, so that the magnitude of the temperature gradient in the bath liquid is very small, even for a finite heat flux. This is an inherent characteristic of an ideal heat bath. So there can be heat flow in the bath to- and from the boundary even though the temperature gradient is tiny.
what causes the transfer of heat?
the different temperature between the gas and the system boundary created a heat flow?
- #31
- 23,280
- 5,682
If the gas is compressed, its temperature rises above that of the bath fluid, or if is expanded the opposite happens. Or if you electrically heat the gas, the temperature will rise above that of the bath fluid. Another example is a chemical reaction in the gas that is exotheic or endothermic. This all results in heat flow. So the heat flow is the effect, not the cause.tze liu said:oh i see
what causes the transfer of heat?
the different temperature between the gas and the system boundary created a heat flow?
- #32
tze liu
- 57
- 0
thank youChestermiller said:If the gas is compressed, its temperature rises above that of the bath fluid, or if is expanded the opposite happens. Or if you electrically heat the gas, the temperature will rise above that of the bath fluid. Another example is a chemical reaction in the gas that is exotheic or endothermic. This all results in heat flow. So the heat flow is the effect, not the cause.
i get confused in this part also
did they do something wrong?
for example Cv=(dQ/dT)v=T(dS/dT)v
however this is true only for reversible process
but the question doesn't state it is reversible
Attachments
- #33
- 23,280
- 5,682
The equation should really read $$C_v=\left(\frac{\partial U}{\partial T}\right)_v=T\left(\frac{\partial S}{\partial T}\right)_v$$ This a physical property relationship for the material that applies to any process. The problem with the example is the Q in the equation, which is path-dependent.tze liu said:thank you
i get confused in this part also
did they do something wrong?
for example Cv=(dQ/dT)v=T(dS/dT)v
however this is true only for reversible process
but the question doesn't state it is reversible
- #34
tze liu
- 57
- 0
do u think the Q in the textbook here is wrong also?Chestermiller said:The equation should really read $$C_v=\left(\frac{\partial U}{\partial T}\right)_v=T\left(\frac{\partial S}{\partial T}\right)_v$$ This a physical property relationship for the material that applies to any process. The problem with the example is the Q in the equation, which is path-dependent.
- #35
tze liu
- 57
- 0
but the definition of heat capacity is not dU/dt but dQ/dt~~Chestermiller said:The equation should really read $$C_v=\left(\frac{\partial U}{\partial T}\right)_v=T\left(\frac{\partial S}{\partial T}\right)_v$$ This a physical property relationship for the material that applies to any process. The problem with the example is the Q in the equation, which is path-dependent.
Similar threads
- Replies
- 24
- Views
- 2K
-
Thermodynamics
- Replies
- 8
- Views
- 994
- Replies
- 4
- Views
- 998
-
Mechanics
- Replies
- 34
- Views
- 3K
-
Introductory Physics Homework Help
- Replies
- 8
- Views
- 1K
-
Advanced Physics Homework Help
- Replies
- 3
- Views
- 939
-
Mechanics
- Replies
- 2
- Views
- 997
-
Mechanics
- Replies
- 16
- Views
- 1K
- Replies
- 20
- Views
- 1K
-
Materials and Chemical Engineering
- Replies
- 1
- Views
- 3K
Share:

