lando45
- 84
- 1
I am a little confused. I was talking to my teacher a couple days ago, and he asked me to put the following three into order of velocity (greatest first):
1. Average velocity of the molecules in a gas (AV)
2. Most probable velocity of the molecules in a gas (MPV)
3. RMS (root mean square) velocity of the molecules in a gas (RMSV)
Well, I thought that AV and MPV must be the same? Because surely the MPV is based upon the AV? And then the formula used to calculate RMSV is:
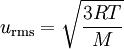
So I figured this is greater than the other 2? So I said to him RMSV had the greatest velocity, and then AV and MPV had equal velocities, but he told me this was incorrect. Can anyone help me out? Are they all equal?
1. Average velocity of the molecules in a gas (AV)
2. Most probable velocity of the molecules in a gas (MPV)
3. RMS (root mean square) velocity of the molecules in a gas (RMSV)
Well, I thought that AV and MPV must be the same? Because surely the MPV is based upon the AV? And then the formula used to calculate RMSV is:
So I figured this is greater than the other 2? So I said to him RMSV had the greatest velocity, and then AV and MPV had equal velocities, but he told me this was incorrect. Can anyone help me out? Are they all equal?