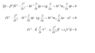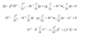You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
A Which Transform to Use for Solving Thermoelastic PDEs?
- A
- Thread starter mohammed El-Kady
- Start date
Physics news on Phys.org
magoo
- 167
- 45
You need to try something to see if you are on the right track. We can't just give you the solution.
What do you know about Fourier or Laplace transforms?
What do you know about Fourier or Laplace transforms?
mohammed El-Kady
- 32
- 2
Sorry I was busy a bit
I put my solution i don't its true or false .. i used the laplace trans. then Fourier tran.
sorry for the line sorry for the camera
if the solution is true I've 2 problems
1- I cannot find the inverse of laplace and fourier
2- I cannot write this system on the matlab
so sorry again
I put my solution i don't its true or false .. i used the laplace trans. then Fourier tran.
sorry for the line sorry for the camera
if the solution is true I've 2 problems
1- I cannot find the inverse of laplace and fourier
2- I cannot write this system on the matlab
so sorry again
Attachments
I sketched the isoclines for $$ m=-1,0,1,2 $$. Since both $$ \frac{dy}{dx} $$ and $$ D_{y} \frac{dy}{dx} $$ are continuous on the square region R defined by $$ -4\leq x \leq 4, -4 \leq y \leq 4 $$ the existence and uniqueness theorem guarantees that if we pick a point in the interior that lies on an isocline there will be a unique differentiable function (solution) passing through that point. I understand that a solution exists but I unsure how to actually sketch it. For example, consider a...
Similar threads
- Replies
- 1
- Views
- 3K
- Replies
- 4
- Views
- 3K
- Replies
- 3
- Views
- 3K
- Replies
- 5
- Views
- 3K
- Replies
- 4
- Views
- 2K
- Replies
- 9
- Views
- 3K
- Replies
- 3
- Views
- 589
- Replies
- 1
- Views
- 1K
- Replies
- 4
- Views
- 3K
- Replies
- 2
- Views
- 2K
Hot Threads
-
I Understanding Legendre differential equation
- Started by chwala
- Replies: 2
- Differential Equations
-
I Visual Representation of Separation of Varables
- Started by sonnichs
- Replies: 4
- Differential Equations
-
A Searching for radial part solution of Klein-Gordon type equation
- Started by art1915
- Replies: 1
- Differential Equations
-
I Why Lagrange’s method of solving Pp + Qq=R works?
- Started by PLAGUE
- Replies: 3
- Differential Equations
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math