milesyoung
- 818
- 67
Hi,
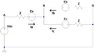
I have attached a diagram of a wye connected motor load with open neutral. The circuit shows an inverter state with a DC-bus voltage from terminal A to G (ground). The following equations should hold:
V_AN = Z*Ia + Ea
V_GN = Z*Ib + Eb
V_GN = Z*Ic + Ec
Ia + Ib + Ic = 0
Ea + Eb + Ec = 0 (back EMFs sum to zero)
I want to prove that:
Ea/Ia = Eb/Ib = Ec/Ic
which would mean, according to:
V_AN/Ia = Z + Ea/Ia
V_GN/Ib = Z + Eb/Ib
V_GN/Ic = Z + Ec/Ic
that the impedance + back EMF in each phase can be replaced by the same effective impedance. I have verified this by simulation in LTspice.
This is probably very simple, but it has been bothering me all day. Any help is greatly appreciated.
Thanks!
I have attached a diagram of a wye connected motor load with open neutral. The circuit shows an inverter state with a DC-bus voltage from terminal A to G (ground). The following equations should hold:
V_AN = Z*Ia + Ea
V_GN = Z*Ib + Eb
V_GN = Z*Ic + Ec
Ia + Ib + Ic = 0
Ea + Eb + Ec = 0 (back EMFs sum to zero)
I want to prove that:
Ea/Ia = Eb/Ib = Ec/Ic
which would mean, according to:
V_AN/Ia = Z + Ea/Ia
V_GN/Ib = Z + Eb/Ib
V_GN/Ic = Z + Ec/Ic
that the impedance + back EMF in each phase can be replaced by the same effective impedance. I have verified this by simulation in LTspice.
This is probably very simple, but it has been bothering me all day. Any help is greatly appreciated.
Thanks!