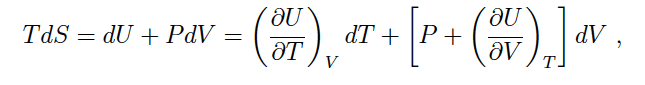thegirl
- 40
- 1
when expressing dS as a function of dV and dT, dU was expanded out as you can see in the screenshot below, is there a mathematical rule which allows this? does the fact that the internal energy is expanded out change the meaning of the expression?