Why Can't Forces Replace Energy Conservation for Spring Stretch?

[CaglarKorkmazgoz]

Homework Statement

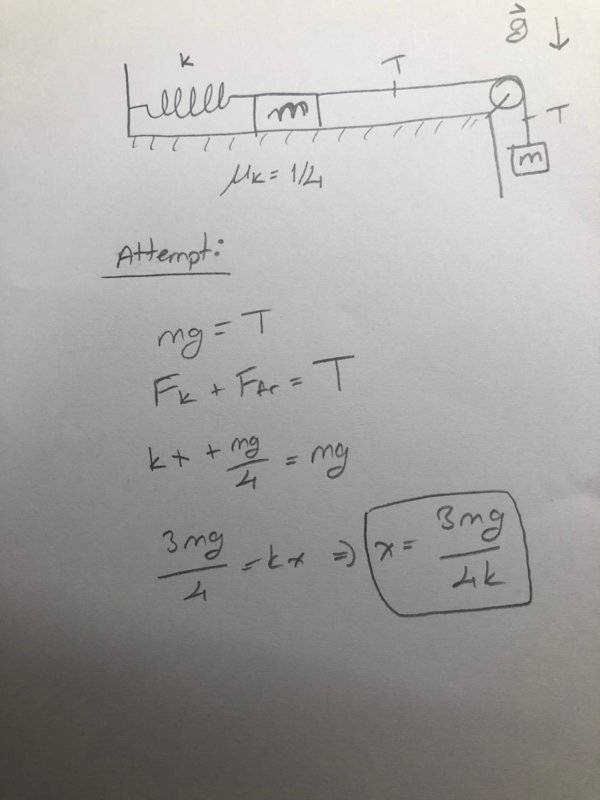
Find the stretch of spring (x=L)

Relevant Equations

mg=T
mg=mgu+kx
mg=(mg/4)+kx
(3mg/4k)=x=L

Hello, I am new on this forum, so if I make any mistakes please inform me. Thank you.

I wonder why I cannot use forces instead of energy conservation in this question.
The question is:
"How far (x = L) does the spring stretch before the masses stop moving? Express your answer in terms of m, k and some constants as needed."

Here is my attempt but of course it is wrong (I imagined the last situation which is equilibrium), the answer should be (3mg)/2k:

 

[Doc Al]

I wonder why I cannot use forces instead of energy conservation in this question.

Because once released, the hanging mass will drop beyond the equilibrium point. You are solving for the maximum stretch, not the equilibrium position. (At least that's what I presume they are asking for.)

 

[CaglarKorkmazgoz]

Because once released, the hanging mass will drop beyond the equilibrium point. You are solving for the maximum stretch, not the equilibrium position. (At least that's what I presume they are asking for.)

I think the problem is the difference between the coefficient of kinetic and static frictions, but I will think about that. Thank you

 

[Doc Al]

I think the problem is the difference between the coefficient of kinetic and static frictions, but I will think about that. Thank you

The request "How far (x = L) does the spring stretch before the masses stop moving?" is a bit ambiguous. I assumed they meant momentarily stop moving, but it's unclear. (I see no mention of static friction here.)

 

[CaglarKorkmazgoz]

(I see no mention of static friction here.)

At final, it will stop moving, so there will not be any kinetic friction, it will be static friction I guess. But the only given quantity is about coefficient of kinetic friction so that when I try to use "Force equality" it gives me a wrong answer.

 

[Doc Al]

If you interpret the question as I did, you'll get the "right" answer.

 

[haruspex]

At final, it will stop moving, so there will not be any kinetic friction

Until it has stopped moving, at least instantaneously, it is kinetic friction. So static friction has no relevance to how far it moves. You would need to know the static friction if you wanted to find out whether it then starts to move back again.

when I try to use "Force equality" it gives me a wrong answer

That's because that method overlooks the momentum built up during the expansion of the spring.
If, instead, you wanted to know how far away you could carefully position the mass without its then moving to the left you would have used spring force balancing static friction.

 

[CaglarKorkmazgoz]

Until it has stopped moving, at least instantaneously, it is kinetic friction. So static friction has no relevance to how far it moves. You would need to know the static friction if you wanted to find out whether it then starts to move back again.

That's because that method overlooks the momentum built up during the expansion of the spring.
If, instead, you wanted to know how far away you could carefully position the mass without its then moving to the left you would have used spring force balancing static friction.

Thank you so much for the explanation