noamriemer
- 50
- 0
Hi there! I'm having trouble understanding the transistor circuit analysis. Hope you could help me :)
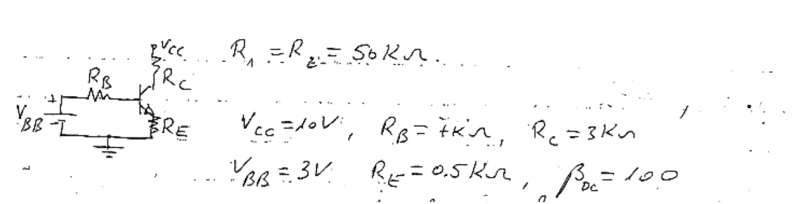
First I need to find the active region of the transistor. What I saw in the solutions was an assumption that the transistor is in saturation region and then:
VBB=IbRb+Vbe+IeRe
Vcc=IcRc+Vce+IeRe
Why did the solver assume the transistor is in saturation mode, when he is supposed to find the active region?
Next, I have to calculate the minimal RE needed for the transistor to be active.
This time, they did refer to it as in active region. But, the equations remained the same. I thought that in Active region, it is supposed to reverse:
VBB=IbRb+Vbe+IeRe
Vce-IcRc-Vcc=IeRe
Why isn't there any change in the equations ? the BC diode is supposed to be in reverse mode, isn't it ?
Thank you!
First I need to find the active region of the transistor. What I saw in the solutions was an assumption that the transistor is in saturation region and then:
VBB=IbRb+Vbe+IeRe
Vcc=IcRc+Vce+IeRe
Why did the solver assume the transistor is in saturation mode, when he is supposed to find the active region?
Next, I have to calculate the minimal RE needed for the transistor to be active.
This time, they did refer to it as in active region. But, the equations remained the same. I thought that in Active region, it is supposed to reverse:
VBB=IbRb+Vbe+IeRe
Vce-IcRc-Vcc=IeRe
Why isn't there any change in the equations ? the BC diode is supposed to be in reverse mode, isn't it ?
Thank you!