Why do masses on a disk move differently than masses on a string?

[PFuser1232]

Homework Statement

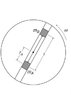
A disk rotates with constant angular velocity $ω$, as shown (attached image). Two masses, $m_A$ and $m_B$, slide without friction in a groove passing through the center of the disk. They are connected by a light string of length $l$, and are initially held in position by a catch, with mass $m_A$ at distance $r_A$ from the center. Neglect gravity. At $t = 0$ the catch is removed and the masses are free to slide.

Find $\ddot{r}_A$ immediately after the catch is removed, in terms of $m_A$, $m_B$, $l$, $r_A$, and $ω$.

Homework Equations

$$\sum_{}^{} \vec{F}_r = m(\ddot{r} - r \dot{\theta}^2) \hat{r}$$

3. The Attempt at a Solution

The particles are constrained to move according to $r_A + r_B = l$. Differentiating twice with respect to time, we get $\ddot{r}_A = -\ddot{r}_B$. Each particle experiences a force of magnitude $T$ where $T$ is the tension in the string. Writing down the equations of motion:
$$-T = -m_A(\ddot{r}_A - r_A \omega^2)$$
$$-T = -m_B(\ddot{r}_B - r_B \omega^2)$$
Eliminating $T$ and substituting $r_B = l - r_A$ and $\ddot{r}_B = -\ddot{r}_A$ we get:
$$\ddot{r}_A = \omega^2 \frac{m_A r_A + m_B r_A - m_B l}{m_A + m_B}$$
Is this answer correct?
Also, before $t = 0$, were $m_A$ and $m_B$ acted upon by an additional force $F$ such that $|F - T| = mr\omega^2$? Or was the string fixed?
It seems to me that my physical intuition was wrong (again). I don't understand why the $\ddot{r}$ terms appear in the equations of motion. Why can't the masses remain at a fixed distance from the circle?
My last question is really about the polar coordinate system and the constraint I used above, namely $l = r_A + r_B$.
If the disk was big enough, and the string was entirely on one side of the circle (the origin no longer lies on the string), then we would be forced to interpret the radial coordinate of the particle closer to the pole as negative, otherwise the sum of the radial coordinates would not equal the length of the string, right?
Sometimes, I find the non-uniqueness of polar coordinates really frustrating

 

[mfb]

Is this answer correct?

Looks correct.

We don't know how the system was hold in place before t=0, I don't see how this would matter.

Why can't the masses remain at a fixed distance from the circle?

They can, if their forces are in equilibrium?

If the disk was big enough, and the string was entirely on one side of the circle (the origin no longer lies on the string), then we would be forced to interpret the radial coordinate of the particle closer to the pole as negative, otherwise the sum of the radial coordinates would not equal the length of the string, right?

That, or change the equation for l (and for the force balances) to keep two positive radial distances.

 

[PFuser1232]

Looks correct.

We don't know how the system was hold in place before t=0, I don't see how this would matter.

They can, if their forces are in equilibrium?

That, or change the equation for l (and for the force balances) to keep two positive radial distances.

Why do the particles move around in a spiral, rather than a circle?

 

[haruspex]

Why do the particles move around in a spiral, rather than a circle?

Assuming they move in a circle, you can consider the forces on one and deduce the tension in the string. Likewise the other. If the two tensions are not the same then your assumption must be false.

 

[PFuser1232]

Assuming they move in a circle, you can consider the forces on one and deduce the tension in the string. Likewise the other. If the two tensions are not the same then your assumption must be false.

The two tensions are the same, since the string is massless. What I'm asking is: why are there $\ddot{r}$ terms in the equations of motion in the first place?

 

[haruspex]

The two tensions are the same, since the string is massless. What I'm asking is: why are there $\ddot{r}$ terms in the equations of motion in the first place?

You seem to be saying you want an explanation for the $\ddot r$ term in $|\Sigma F_r| = m(\ddot r - r {\dot \theta}^2)$. Is that right? You should be able to find a derivation online.

 

[PFuser1232]

You seem to be saying you want an explanation for the $\ddot r$ term in $|\Sigma F_r| = m(\ddot r - r {\dot \theta}^2)$. Is that right? You should be able to find a derivation online.

I'm quite familiar with the derivation of acceleration in polar coordinates.
I'm just wondering why it appears in some cases, but not others.

 

[haruspex]

I'm quite familiar with the derivation of acceleration in polar coordinates.
I'm just wondering why it appears in some cases, but not others.

Well, it will be zero for circular motion of course. Can you list some other case?