MironeDagains
- 23
- 0
Homework Statement
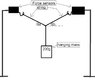
There's a 200g piece of weight hanging by a string. That string is then split into two strings, each at θ from the horizontal and Φ from the horizontal. These two strings are each connected to force sensors which measure their tension in Newtons. I know how to do this problem, as it's a simple trigonometric or pythagoras problem. The problem I'm having, is the fact that my answers are completely different to what my teacher got. She actually used real sensors and wrote down what she saw when she tested each θ and Φ.
Maybe I don't know what I'm talking about, or maybe my teacher's force sensor is faulty. You decide.
Here's a diagram: http://i.imgur.com/439esTg.png
Homework Equations
F=mg
sin(θ)x0.2kgx9.8=NF1
sin(Φ)x0.2kgx9.8=NF2
Triangles, sin cos tan
The Attempt at a Solution
F1: sin θ x 0.2kg x 9.8
F2: sin Φ x 0.2kg x 9.8
Here's an image of my method. Please let me know whether it's correct or not. http://i.imgur.com/LTbo8Q9.jpg I cannot reproduce them as words here, as they are almost all diagrams.
Note: The columns "Force F1 measured", "Angle θ", "Force F2 measured" and "Angle Φ" were already pre-filled when I was handed this worksheet. The only things I filled in were the "Force F1 calculated" and "Force F2 calculated". You will notice how incredibly 'off' my calculated measurements are from her measured measurements.
So, am I going insane? Or does my teacher need to invest in a new force sensor?
Thank you