gprd3
- 4
- 0
I am having trouble understanding short circuits and would appreciate some help with it.
From what I understand, a short circuit occurs when we have a connection with a very low (zero) resistance is made between two points in a circuit. With R=0, the only resistance in our circuit would be the internal resistance of the battery. This causes a large current to go through the circuit Any clarifications, corrections, or additional information is greatly appreciated.
I also had trouble solving a homework problem that uses this concept. The following is the problem:
In the circuit below, all four resistors are identical (R1 = R2 = R3 = R4 = R) and the battery has a voltage of 5.17 V.
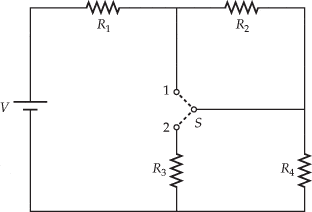
(a) When the switch is placed in position 1, the measured current in the battery is 1.14 mA. What is the value of each resistor?
[; I=V/R;]
For resistors in series:
[;R_t_o_t=R_1+R_2;]
For resistors in paraller:
[;R_t_o_t=(1/R_1+1/R_2)^-^1;]
Finding the total resistance of the circuit using Ohm's Law is easy:
[;R_t_o_t=V/I=5.17 V/1.14e^3 A= 4.54e^3 ohm;]
I then use [;R_t_o_t=R_1+R_2+R_3+R_4;] to find an expression for the total resistance in terms of R. Using this second equation with the value found with the first equation allows me to find R.
It turns out that [;R_2;] and [;R_3;] are both equal to zero! This is what I don't understand; WHY are they zero? I believe it has something to do with short circuits but I don't really understand what.
I appreciate your help.
From what I understand, a short circuit occurs when we have a connection with a very low (zero) resistance is made between two points in a circuit. With R=0, the only resistance in our circuit would be the internal resistance of the battery. This causes a large current to go through the circuit Any clarifications, corrections, or additional information is greatly appreciated.
I also had trouble solving a homework problem that uses this concept. The following is the problem:
Homework Statement
In the circuit below, all four resistors are identical (R1 = R2 = R3 = R4 = R) and the battery has a voltage of 5.17 V.
(a) When the switch is placed in position 1, the measured current in the battery is 1.14 mA. What is the value of each resistor?
Homework Equations
[; I=V/R;]
For resistors in series:
[;R_t_o_t=R_1+R_2;]
For resistors in paraller:
[;R_t_o_t=(1/R_1+1/R_2)^-^1;]
The Attempt at a Solution
Finding the total resistance of the circuit using Ohm's Law is easy:
[;R_t_o_t=V/I=5.17 V/1.14e^3 A= 4.54e^3 ohm;]
I then use [;R_t_o_t=R_1+R_2+R_3+R_4;] to find an expression for the total resistance in terms of R. Using this second equation with the value found with the first equation allows me to find R.
It turns out that [;R_2;] and [;R_3;] are both equal to zero! This is what I don't understand; WHY are they zero? I believe it has something to do with short circuits but I don't really understand what.
I appreciate your help.