Why does Griffiths use a vector to explain angular frequency of rotation?

[yungman]

This is an example from the book and it is not a homework. There is one part of the step I just don't get. This is the question on page 236 of Griffiths "Introduction to Electrodynamics":

Example 5.11

A spherical shell, of radius R, carrying a uniform surface charge $\rho$, is set spinning at angular velocity $\omega$. Find vector magnetic potential it produces at a point r.

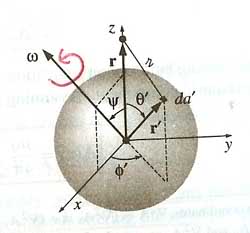
The book setup so the point is on the z axis and let the sphere spin on axis in the xz plane where the axis of spin make an angle $\psi$ with the +ve z axis. The equation used is:

$$\vec A \;=\; \frac {\mu_0}{4\pi} \int_{s'} \frac {\rho \vec v }{\sqrt { R^2 +r^2 -2Rrcos \theta'}} dv'$$

$$\vec v \;=\; \vec {\omega} \;X\; \vec r \;' \;\hbox { where }\; \vec {\omega} =\hat x [\omega \;sin (\psi)] + \hat z [\omega \;cos (\psi)]$$ (1)

I don't understand how the book arrive to (1)

My question is how do you go from a sphere spinning on the axis at direction of $( \omega sin \psi, 0, \omega cos \psi )$ to just a vector of $\omega$?

Can anyone explain to me how they arrive the velocity vector $\vec v$?

Thanks

 

[tiny-tim]

hi yungman!

(have an omega: ω )

My question is how do you go from a sphere spinning on the axis at direction of $( \omega sin \psi, 0, \omega cos \psi )$ to just a vector of $\omega$?

but that's the definition of angular velocity …

if the angular velocity of a body is the vector ω, then the velocity of a point at position vector r is ω x r

 

[yungman]

hi yungman!

(have an omega: ω )


but that's the definition of angular velocity …

if the angular velocity of a body is the vector ω, then the velocity of a point at position vector r is ω x r

Hi Tiny-Tim, thanks for the info. I search through books that cover the first three semesters calculus including multi-variables, ODE, PDE, Advance calculus and Vector calculus. I only find one example on angular velocity. No wonder I am so loss on this. I don't even have a book for this.

I got the info on Wikipedia. What class is the angular velocity taught? I thought I have enough math background for the Griffiths' book after I study PDE!

Thanks for your time.

Alan

 

[tiny-tim]

What class is the angular velocity taught?

i've no idea, but i think you need an elementary book on manipulating vectors (dot and cross products etc)

 

[RedX]

I got the info on Wikipedia. What class is the angular velocity taught?

Classical mechanics. But I believe you can learn electrodynamics before classical mechanics, so it doesn't really matter the order.

For instantaneous rotation about a fixed axis, a (skew-symmetric) operator takes a point in the fixed frame and maps it to the velocity in the fixed frame:

$$\left(\begin{array}{c}<br /> \dot{q_1}\\<br /> \dot{q_2}\\<br /> \dot{q_3}<br /> \end{array}<br /> \right)<br /> =<br /> <br /> \left(<br /> \begin{array}{ccc}<br /> 0 & -\omega_3 & \omega_2\\<br /> \omega_3 & 0 & -\omega_1 \\<br /> -\omega_2 & \omega_1 & 0<br /> \end{array}<br /> \right)<br /> <br /> \left(\begin{array}{c}<br /> q_1\\<br /> q_2 \\<br /> q_3<br /> \end{array}<br /> \right)$$

Or as noted: $$\dot{\vec{q}}=\vec{\omega} \mbox{x} \vec{q}$$

 

[yungman]

i've no idea, but i think you need an elementary book on manipulating vectors (dot and cross products etc)

I find it in one of the vector calculus book ( not the regular calculus book used in the first semister classes). It only show as an example, not even in regular chapter! Two other vector calculus books don't even have this. It is very easy once I know the definition and derivation.

Thanks

 

[yungman]

I have a second question from this same problem. I followed and worked out all the way to get A at the point both inside and outside of the rotating charged sphere |R>r| and |r>R| resp.

The book than want to get the more general solution where they let $\vec {\omega}$ be on the z-axis and the point be any random point (x,y,z). I cannot verify what the book's answer. Please help. From calculation as in my original post where the point $P_{\vec r}$ is on the z-axis and the $\vec {\omega}$ is in the xz plane making angle $\psi$ with the z-axis as shown in post #1:

$$\vec A_{(\vec r)} = -\hat y \frac {R^4 \omega \rho_s \mu_0 sin \psi }{3r^2} \;\hbox { for r bigger than R.}$$ (3)

$$\vec A_{(\vec r)} = -\hat y \frac {R r \omega \rho_s \mu_0 sin \psi }{3} \;\hbox { for R bigger than r.}$$ (4)


$$\vec{\omega} \;X\; \vec r \;=\; -\hat y r \omega sin \psi$$

Substitude into (3) & (4)

$$\vec A_{(\vec r)} = \frac {R^4 \rho_s \mu_0 }{3r^2} (\vec{\omega} \;X\; \vec r) \;\hbox { for r bigger than R.}$$ (5)

$$\vec A_{(\vec r)} = \frac {R \rho_s \mu_0 }{3} (\vec{\omega} \;X\; \vec r) \;\hbox { for R bigger than r.}$$ (6)

The above is in rectangular coordinates, the answer is consistance with the book so it is correct. The next step is where I get lost. The book want to derive the formulas for the point P in any position with $\vec \omega$ on z-axis. The book gave this as answer:

$$\vec A_{(r,\theta, \phi)} \;=\; \hat {\phi}\; \frac {R^4 \rho_s \mu_0 \omega sin \theta}{3r^2} \;\hbox { for r bigger than R.}$$ (7)

$$\vec A_{(r,\theta, \phi)} \;=\; \hat {\phi}\; \frac {R \rho_s \mu_0 \omega r sin \theta}{3} \;\hbox { for R bigger than r.}$$ (8)


Below is what I tried to do and I just cannot get the answer of the book's example:

From (5) & (6), the vector position is only contained in $(\vec {\omega} \;X\; \vec r)$. So I just have to calculate this cross product in spherical coordinates with $\vec {\omega}$ on z-axis and $\vec r_{(R,\theta,\phi)} = (r_R, r_{\theta}, r_{\phi})$.

To convert $\vec{\omega} = \hat z \omega$ in rectangular coordinates to spherical coordinates, I use:

$$\hat R =\hat x sin \theta cos \phi \;+\; \hat y sin \theta sin \phi \;+\; \hat z cos \theta, \;\;\;\hat {\theta} =\hat x cos \theta cos \phi \;+\; \hat y cos \theta sin \phi \;-\; \hat z sin \theta, \;\;\;\hat {\phi} =-\hat x sin \phi \;+\; \hat y cos \phi$$

To find each of the magnitude of each components of $\vec{\omega}$ in spherical coordiantes:

$$\omega_R \;=\; \vec {\omega} \cdot \hat R = \omega cos \theta, \;\;\;\omega_{\theta} \;=\; \vec {\omega} \cdot \hat {\theta} = -\omega sin \theta, \;\;\;\omega_{\phi} \;=\; \vec {\omega} \cdot \hat {\phi} = 0$$

$$\vec {\omega}_{(x,y,z)}= \hat z {\omega} \;\Rightarrow\; \theta =0 \;\Rightarrow\; sin \theta =0,\;\; cos \theta =1$$

$$\Rightarrow \; \vec {\omega} _{(R,\theta,\phi)} \;=\; \hat R \omega, \;\;\hbox { and from above }\; \vec r_{(R,\theta,\phi)} = (r_R, r_{\theta}, r_{\phi})$$

$$\vec {\omega}_{(R,\theta,\phi)} \;X\; \vec r_{(R,\theta,\phi)} \;= -\;\hat {\theta} \omega r_{\phi} \;+\;\hat {\phi} \omega r_{\theta}$$

As you can see, I have all three components instead of what the book's answer that only contain the $\hat {\phi}$ component in (7) & (8).

What did I do wrong? I double check my work on the conversion already. Please help.

Thanks

Alan