Why Does Kinematics Fail in Calculating Fmax in This Physics Problem?

[xstetsonx]

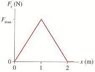
A 400 g particle moving along the x-axis experiences the force shown in Figure Ex11.15. The particle goes from vx = 2.5 m/s at x = 0 m to vx = 5.5 m/s at x = 2 m. What is Fmax?

my solution manual told me to do this with work and energy

but why can't i do
kinematic:
5.5^2=2.5^2+2A2=6

F=ma
(0.4KG)(6m/s^2)=.5Fmax(2)=2.4N
area under the curve--triangle---

but the correct answer is 4.8N...ugh

 

[xstetsonx]

Wait the area underneath the curve is work right and my answer is the total force? ... so i have to do W=(F)(delta X)??

 

[willem2]

If the curve had the force as a function of time then your approach would work.

m(v_2-v_1) = \int_{t_1}^{t_2} F(t) dt

this is simply F=ma integrated

but since it isn't you can't do this and you will have to use

W = \int_{x_1}^{x_2} F(x) \cdot dx