Why Does Moving the Microscope Objective Create a Second Image?

Click For Summary
SUMMARY

The discussion centers on the optical phenomenon observed when a microscope objective (M) is moved while maintaining focus, resulting in the formation of a second image of a scratch on a transparent plate. The key factors include the thickness (t) and refractive index (n) of the plate, as well as the distance (D) from the objective to the image point (A'). The movement of the objective (d) does not alter the distance D, allowing light to reflect and refract in a manner that produces an additional sharp image of the scratch at a different location. This phenomenon is attributed to the principles of reflection and refraction in optics.

PREREQUISITES
  • Understanding of optical principles, specifically reflection and refraction.
  • Familiarity with microscope objectives and their imaging properties.
  • Knowledge of basic geometrical optics, including image formation.
  • Concept of light propagation through transparent media with varying refractive indices.
NEXT STEPS
  • Study the principles of light reflection and refraction in detail.
  • Explore the optical characteristics of microscope objectives, including their design and function.
  • Investigate the effects of varying the distance between the objective and the specimen on image formation.
  • Learn about the mathematical modeling of image formation in optical systems.
USEFUL FOR

This discussion is beneficial for students studying optics, optical engineers, and anyone interested in the behavior of light in microscopy and imaging systems.

Numen
Messages
2
Reaction score
0

Homework Statement


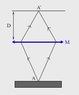
I have a transparent plate (call the thickness t and refractive index n), it has a scratch at a point A. A microscope objective (M, positive) images the point A in A' at a distance D from the objective. If we move M a certain distance d down (without changing focus, meaning D is unchanged), there will be another sharp image of the scratch.

How come?

Homework Equations



Not needed?

The Attempt at a Solution



I was thinking that it might be some reflection on the objective that reflects the light back to the plate and back to the objective at the same point as before it was moved, and then refracted towards A'. I'm not sure if I understand the problem correctly... I think it is suggesting a second image somewhere else?
 
Physics news on Phys.org
Ok, I tried illustrating the problem. Please check the attachment (hope it helps).
 

Attachments

  • p2.jpg
    p2.jpg
    4.2 KB · Views: 494

Similar threads

Ray optics: velocity of image reflected off a moving mirror
  • · Replies 5 ·
Replies
5
Views
2K
Microscope Optics: questions and calculations
  • · Replies 12 ·
Replies
12
Views
2K
Number of Images Formed from Reflection & Refraction
  • · Replies 3 ·
Replies
3
Views
1K
Is the Solution for Rotation of Spherical Mirrors Incorrect?
  • · Replies 16 ·
Replies
16
Views
2K
Could the Image from the First Mirror Be Real for the Second Mirror?
  • · Replies 7 ·
Replies
7
Views
2K
A problem involving thin film interference
  • · Replies 2 ·
Replies
2
Views
2K
Imaging resolution for a microscope and eye
  • · Replies 5 ·
Replies
5
Views
2K
Inserting thick lenses into a thin lens system and deducing values
  • · Replies 1 ·
Replies
1
Views
2K
Position of the object and image in this optics problem
  • · Replies 10 ·
Replies
10
Views
2K
The focal length of a microscope eyepiece
  • · Replies 1 ·
Replies
1
Views
3K