pyroknife
- 611
- 4
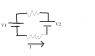
I have attached the circuit of interest.
The 2 resistors of of resistance R. V1 and V2 are the voltage sources. 'I' is the current we're solving for.
Using KVL, we get:
-V1-R*I+V2-R*I=0
Rearranging:
V1-V2=-2R*I
(V2-V1)/(2R)=I
My answer doesn't seem to match the solutions. Am I missing something here?
The 2 resistors of of resistance R. V1 and V2 are the voltage sources. 'I' is the current we're solving for.
Using KVL, we get:
-V1-R*I+V2-R*I=0
Rearranging:
V1-V2=-2R*I
(V2-V1)/(2R)=I
My answer doesn't seem to match the solutions. Am I missing something here?