eraserxp
- 10
- 0
\frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty}\frac{e^{\beta(\varepsilon_{F}-\varepsilon_i)}}{\beta}d\beta=?
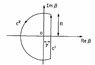
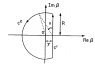
When \varepsilon_{F}>\varepsilon_{i}, the contour is C1 + C2 (see the attached file). Let \beta\rightarrow \infty, the integration along C2 vanishes. Then the result is given by the value of e^{\beta(\varepsilon_{F}-\varepsilon_i)}/\beta at pole \beta=0, which is 1.
The problem is that I don't understand why the contribution from C2 vanishes when \beta approaches infinity. It seems to me that
\int_{C^2}\frac{e^{\beta(\varepsilon_{F}-\varepsilon_i)}}{\beta}d\beta \leq \lim _{\beta\rightarrow \infty}\left|\frac{e^{\beta(\varepsilon_{F}-\varepsilon_i)}}{\beta}\right|\lim_{\beta\rightarrow \infty} \left|d\beta\right|_{\gamma-i\infty}^{\gamma+i\infty}=\infty\cdot\infty
The above equation doesn't rule out the possibility for the integration to be zero, but it still confuses me.
When \varepsilon_{F}>\varepsilon_{i}, the contour is C1 + C2 (see the attached file). Let \beta\rightarrow \infty, the integration along C2 vanishes. Then the result is given by the value of e^{\beta(\varepsilon_{F}-\varepsilon_i)}/\beta at pole \beta=0, which is 1.
The problem is that I don't understand why the contribution from C2 vanishes when \beta approaches infinity. It seems to me that
\int_{C^2}\frac{e^{\beta(\varepsilon_{F}-\varepsilon_i)}}{\beta}d\beta \leq \lim _{\beta\rightarrow \infty}\left|\frac{e^{\beta(\varepsilon_{F}-\varepsilon_i)}}{\beta}\right|\lim_{\beta\rightarrow \infty} \left|d\beta\right|_{\gamma-i\infty}^{\gamma+i\infty}=\infty\cdot\infty
The above equation doesn't rule out the possibility for the integration to be zero, but it still confuses me.
Attachments
Last edited: