Why does this proportion work?

[mathgeek7365]

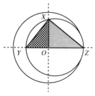
In this diagram, triangleXYZ is inscribed into the circles. O is the center of the larger circle. OZ=x, altitude XO=x-5, and OY=x-9. angleXOZ and angleXOY are both right angles. Using the two similar right triangles OYX, and OXZ, this proportion can be written: OY/OX=OX/OZ
Then: (x-9)/(x-5)= (x-5)/x

My daughter wants to know why this works. How was this proportion written, why it works and how we know triangleOYX is similar to triangleOXZ? We appreciate any information as to why this works.

View attachment 5133

 

[Greg]

By Thales' theorem, $\angle{YXZ}=90^\circ$. As $\angle{XYO}+\angle{XZO}=90^\circ$ and $\angle{XYO}+\angle{YXO}=90^\circ$, $\angle{XZO}=\angle{YXO}$ and triangles $OYX$ and $OXZ$ are similar.