Why Doesn't Total Mechanical Work Equal the Sum of All Work Values?

[scuroangel66]

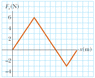
Alright we just learned about work in our physics class and I've met with my professor to try and help me understand the concept better. Here is my question, how much mechanical work is done. The best example would be the diagram I attached. Each block on the graph is 1 unit by 1 unit. I understand total displacement of work gives you your change in K, from the formula W_net=$$\DeltaK$$
The positive area of the graph equals 24J and the negative area of the graph is equal to -6J, so the $$\DeltaK$$=18J That means the work done overall on the system by the force is equal to 18J. But what I don't understand is why he says the object doesn't undergo a total of 30J. Because from x=0 to x=8 the object undergoes 24J and from x=8 to x=12 the object undergoes 6J in the opposite direction. So although the Total Mechanical Work of the system equals 18J, why can't you state the fact that the object underwent a Total Mechanical Work of 30J. I hope I made my thoughts clear. Any help would be great. One other thing I was just thinking was because to find the total are in calculus of an integral, you add the positive and subtract the negative, therefore adding it, giving you 30J from x=0 to x=12. So is there a difference between total displacement (18J of total work of the system) and total area under the curve (30J of work that has been applied to the object between x=0 and x=12)?!?

 

[scuroangel66]

Sorry, there was an error it should read...

W_net=$$\Delta$$K

The positive area of the graph equals 24J and the negative area of the graph is equal to -6J, so the $$\Delta$$K=18J

 

[jackiefrost]

An integration example: If you integrate the function f(x) = sin x from 0 to Pi you'll get 2. Integrating from Pi to 2Pi gives -2. The total is 0.
Integral[sin x] from 0 to 2Pi = 0. The area under the x-axis is negative in sign so quantities like work that depend on totaling the area are algebraically added.

If you specified your graph as four piecewise linear functions of x with domains a<=x<=b:

Function:              Domain:          Integrating the function from a to b: 
f1[x] = 6x/4           a=0,   b=4       12
f2[x] = -6x/4 + 12     a=4,   b=8       12
f3[x] = -6x/4 + 12     a=8,   b=10      -3
f4[x] = 6x/4 - 18      a=10,  b=12      -3

Total work: (Integral[f1], 0 to 4 ) + (Integral[f2], 4 to 8) + (Integral[f3], 8 to 10) + Integral[f4], 10 to 12) = 18