Why Is Calculating Forces on a Truncated Cone's Surfaces Challenging?

[NotaPhysicsMan]

Ahhh Double Star Question...AGAIN!

I think my prof really doesn't like us or maybe he simply has an over expectation of our abilities...

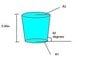
As the drawing shows (attached), a pond has the shape of an inverted cone with the top sliced off and has a depth of 5.00m. The atmospheric pressure is 1.01 x 10^5 PA. The circular top surface (radius=R2) and circular bottom surface (radius=R1) of the pond are both parallel to the ground. The magnitude of the force acting on the top surface is the same as the manitude of the force acting on the bottom surface. Obtain a)R2 and b)R1.

Okay, this looks like the question involving two equations of two unknowns. First I know that F1=F2... So P1A=P2A. The other I believe might have to do with the volume of this pond. A normal cone would have a volume of 1/3pie x r^2 x h. But since this is a cut-off cone, I'm lost here. Also, that 60 degrees is quite confusing. I think it may have to do with the area of the middle section when unfolded, a trapezoid shape perhaps? Any Ideas appreciated!
Thanks.

 

[NotaPhysicsMan]

*bump* Anyone?

 

[dextercioby]

1.Compute the 2 forces and set them equal.Show your work.

Daniel.

 

[NotaPhysicsMan]

ok, so P2 is simply atmospheric pressure which is
1.01 x 10^5. P1 can be found by P2=P1+pgh. That turns out to be pretty much the same as P2, so 1.01 x 10^5. Ok so the pressures P2=P1. Area is pie x r1^2 and pie x r2^2. Ok in terms of force:

F=PA
so P2 x (pie x r2^2)= P1 x (pie x r1^2). Since pie and Pressures are virtually the same, I can cancel them out. So I have r1^2=r2^2 which doesn't make any sense.

 

[dextercioby]

Of course it doesn't.The pressures are DIFFERENT.U can't take them as equal.This is a trick in the problem...


Daniel.

P.S.Post your work again...

 

[NotaPhysicsMan]

P2 x (pie x r2^2)= P1 x (pie x r1^2). <---oK is this at least right? P1 has to be found using this formula, P2=P1+pgh. The pressure at the bottom will definitely be bigger than the top, but only by a factor of pgh, which is 49050. So P1= 1.50 x 10^5 Pa. Ok, now I have the two, now solve for one of the r's. ERR, what's the other equation! I think it may be the volume, some help.

 

[dextercioby]

U don't need the volume.You need to apply the definition of 'tangent'.Think of the rightangle triangle in that trapese.And use the fact that u know ine side of the triangle (namely the height of the trapese) and one angle in the triangle (which is found by using that 60° which the problem gives you).

Daniel.

 

[NotaPhysicsMan]

Yes, I thought that the 60 degrees could be used when you slice the cone in half you get a trapezoid. Maybe I could find the length of one the top or bottom and that would be the circumference. and C=2pie x r. r =C/2pie. I can see how the 60 degrees can be used to find the hypoteneuse and the base but I still can't get the either lengths no matter how many little triangles I cut the thing into...

 

[NotaPhysicsMan]

I just can't seem to get it. HELP

 

[NotaPhysicsMan]

BUMP! I'm still getting no where...

 

[dextercioby]

You don't know geometry,if u can't prove this formula
\tan 30°=\frac{R_{2}-R_{1}}{h}

Then if u don't know geometry,how do u expect solving physics problems??

Daniel.

 

[NotaPhysicsMan]

I did that from the start, but didn't realize that I could simply go R2-R1 and use that as my second equation. I thought I could find an actual number from the 60 degrees..Ah well.