einstein1921
- 76
- 0
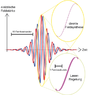
why the pulse is positively chirped pulse in picture 20130320182307.png ? thank you!
I also confused by another picture(20130320183049.png ).Does a femtosecond laser pulse contain a lot of wavelength?if so, a pulse should contains photons which have different energy. why we always say Ti:sappire laser is 800nm?thank you!
I also confused by another picture(20130320183049.png ).Does a femtosecond laser pulse contain a lot of wavelength?if so, a pulse should contains photons which have different energy. why we always say Ti:sappire laser is 800nm?thank you!