Why is the Velocity Too Fast in My Fluids Momentum Conservation Calculation?

[Jaydude]

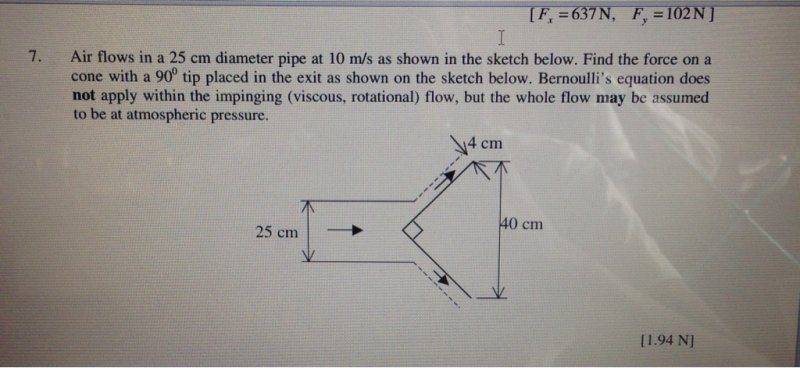
Question with diagram:

Relevant equations:

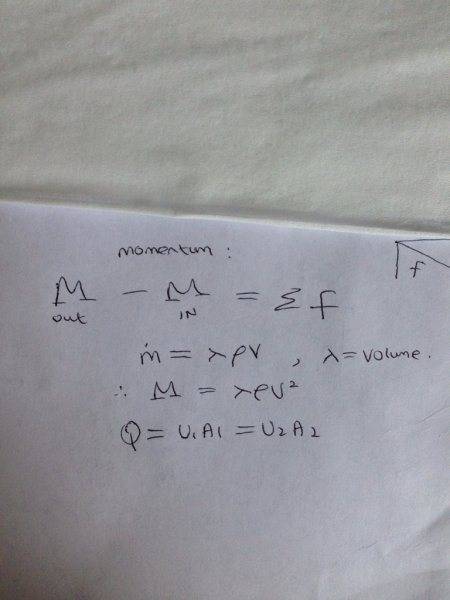
Attempt :

My question:

Using my method I got the wrong force , not sure if in this situation I can use Q=A1U1 = A2U2, hence maybe that's why U2 = 195 m/s looks wrong/too fast?

I continue to use momentum conservation in the x and y directions. Lastly I just used trig to get the resultant force on the cone. I have no idea why we need the 40cm dimension...

Please point me in the right direction!

Thanks and regards,

Jay

 

[Chestermiller]

What is the perimeter of the cone at the location where the diameter is 40 cm. What is the channel cross sectional area at that location if all the flow is contained within the 4 cm channel height? What is the velocity normal to the channel cross section at that location?

Chet