- #1
AishaGirl
- 10
- 0
Hello, AQA is a British exam board and on their paper they have a list of equations. Can someone tell me why the time dilation equation is to the power -1/2?
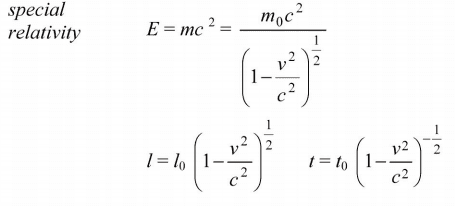
Thanks.
Thanks.
You can get this result in several ways.AishaGirl said:Hello, AQA is a British exam board and on their paper they have a list of equations. Can someone tell me why the time dilation equation is to the power -1/2?
The time dilation equation, t' = t√(1-v²/c²), is raised to the power of -1/2 because it is a result of the Lorentz transformation, which is used to calculate the difference in time between two observers in relative motion. The -1/2 power is derived from the formula for the time dilation factor, γ = 1/√(1-v²/c²), which is then applied to the equation for time dilation.
The time dilation equation is used in many real-life applications, such as in the field of particle physics, where high-speed particles experience time dilation due to their velocity. It is also used in GPS technology, as the satellites in the GPS system experience time dilation due to their high velocity in orbit. Additionally, the equation is used in space travel, where astronauts experience time dilation due to their high speeds relative to Earth.
The time dilation equation is a fundamental part of Einstein's theory of relativity, which revolutionized our understanding of time and space. It is used to explain the difference in time experienced by observers in relative motion and is a key concept in understanding the nature of time and the universe.
The AQA exam board includes the time dilation equation as part of their A-level Physics curriculum, specifically in the topic of Special Relativity. Students are expected to understand the equation, its derivation, and its applications in real-life scenarios.
Like all scientific equations, the time dilation equation has its limitations. It is based on the assumptions of constant velocity and uniform motion, and it does not account for gravitational effects. Additionally, the equation is only accurate for objects traveling at speeds much slower than the speed of light. At very high speeds, more complex equations are needed to accurately calculate time dilation.