String theory guy
- 26
- 4
- Homework Statement
- Why must you measure the COM of a system from the origin before and after a collision?
- Relevant Equations
- COM formula
For example, in the problem below, if the center of mass is chosen to be measured initially at the center of the left mass, then it must be measured from the same position after the collision.

This gives an initial COM of,
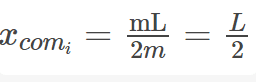
and finial COM of,
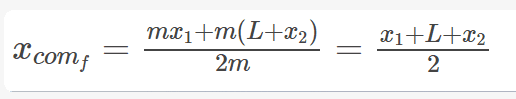
Which gives their change in center of mass of the system.
So why must I find the finial COM of the system with respect to the same place which I used to find the COM before the force was exerted on the system.
This gives an initial COM of,
and finial COM of,
Which gives their change in center of mass of the system.
So why must I find the finial COM of the system with respect to the same place which I used to find the COM before the force was exerted on the system.