riseofphoenix
- 294
- 2
The sport of skateboarding provides an excellent example of the principle of Conservation of Energy. In particular, let us consider 'vert skateboarding' where a person rides the skateboard on a vertical ramp that forms part of a hemisphere referred to as a 'half-pipe.' It consists of the transition from the curved part to the flat and the vertical. Below is a schematic of a half-pipe with the 'vert'. The surface of the half-pipe and the material of the wheels on the skateboard allow for an almost frictionless ride. Therefore we will neglect friction in the following analysis.
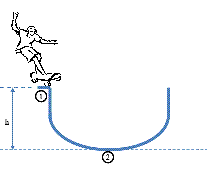
The rider starts from rest at location at the edge of the in-ramp and goes down the transition. Typically, as the rider approaches the flat at location he will crouch down to get his center of mass as low as possible and thus increase his speed. To simplify the problem, let us initially assume that the rider stays upright as he goes down so that his center of mass location relative to his feet does not change from what it was at location . In the following problems, you can use the foot as the unit length instead of meters. Note: g = 32 ft/s2.
Solved!
The rider starts from rest at location at the edge of the in-ramp and goes down the transition. Typically, as the rider approaches the flat at location he will crouch down to get his center of mass as low as possible and thus increase his speed. To simplify the problem, let us initially assume that the rider stays upright as he goes down so that his center of mass location relative to his feet does not change from what it was at location . In the following problems, you can use the foot as the unit length instead of meters. Note: g = 32 ft/s2.
Solved!
Last edited: