Will this door with torsion spring survive?

[thdwngus]

TL;DR Summary

torsion spring design to open a lid with catch

I am trying to design a small box with a hinged door/lid that opens with a torsion spring.
When closed, the door will latch onto a mechanism where the open button is, and when the button is pressed this mechanism will slide away, removing the latch out of the way so that the door can fly open. This is a side view of a hinged door with torsion spring.

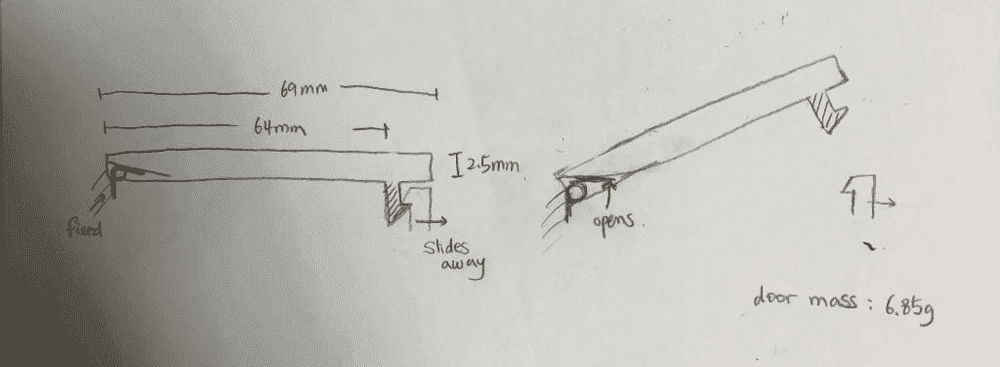
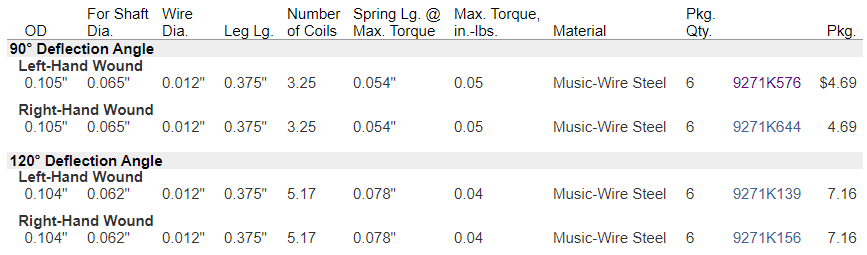
The torsion spring will be preloaded so that it can lift up the door when released, and the door is to open until it reaches a physical stop. I am currently trying to design around a 90 degree or 120 degree torsion spring on both ends of the lid:

It'd be great if I could get any guidance on following questions:
- When in closed state, how much force is exerted on the colored hook? I want to know if the colored hook would fail due to the loaded force of the spring, and would want to prevent that.
- What design specification of the torsion spring is needed for the spring to open the door?

Door mass is 6.85g, please let me know if there are any other information needed. Thanks!

 

[jrmichler]

The force of the spring on the hook will be negligible. The real force happens when you close the lid and it bounces off the box up against the hook. That bounce may be so little that you cannot see it, but it's there and you need to design the hook for it. Similarly, the lid opens against a stop. The weight of the lid against the stop is negligible, but the impact force from the inertia of the moving lid is significant. When designing hooks, latches, and stops in small box lids, design for opening and closing impact forces while ignoring the spring force.

In addition to the size and weight of the door, you need to decide if the spring should slowly open the door or make it fly open with a bang.

The calculation is as follows:
The springs are rated in English units, your box is metric, so translate everything into common units.
Lid weighs 6.85 / 454 = 0.015 lbs
Center of mass of lid is at (69 / 2) / 25.4 = 1.36 inches from hinge.
Torque to barely open lid = 1.36 X 0.015 = 0.020 inch-lbs.
Add about 20% for hinge friction: 0.020 X 1.20 = 0.024 inch-lbs.
If you want the lid to fly open, multiply by 2 or 3.

The above calculation is simplified because it ignores the weight of the hook. A better calculation would use the actual weight of the lid with the hook, then measure the distance from the hinge pin to the center of mass by finding the balance point.

 

[thdwngus]

The force of the spring on the hook will be negligible. The real force happens when you close the lid and it bounces off the box up against the hook. That bounce may be so little that you cannot see it, but it's there and you need to design the hook for it. Similarly, the lid opens against a stop. The weight of the lid against the stop is negligible, but the impact force from the inertia of the moving lid is significant. When designing hooks, latches, and stops in small box lids, design for opening and closing impact forces while ignoring the spring force.

In addition to the size and weight of the door, you need to decide if the spring should slowly open the door or make it fly open with a bang.

The calculation is as follows:
The springs are rated in English units, your box is metric, so translate everything into common units.
Lid weighs 6.85 / 454 = 0.015 lbs
Center of mass of lid is at (69 / 2) / 25.4 = 1.36 inches from hinge.
Torque to barely open lid = 1.36 X 0.015 = 0.020 inch-lbs.
Add about 20% for hinge friction: 0.020 X 1.20 = 0.024 inch-lbs.
If you want the lid to fly open, multiply by 2 or 3.

The above calculation is simplified because it ignores the weight of the hook. A better calculation would use the actual weight of the lid with the hook, then measure the distance from the hinge pin to the center of mass by finding the balance point.

Thanks @jrmichler, this has been really helpful!
One question, why would the force on the hook by the spring be negligible?
When in closed state, since the hook on the door will be held down by the other hook on the bottom, I thought the hook will be the only mechanism that is preventing the door from opening from the preloaded spring, hence a certain constant downward force applied when the door is closed.
I wanted to make sure the hook doesn't break/deflect from trying to stay the door closed, so was wondering about this force. Could you help me out a little bit more?