Will water flow ever stop if we increase resistance?

[Gabriele99]

Complete question:
Will flow ever reverse or stop if we increase resistance in this pipe scenario?

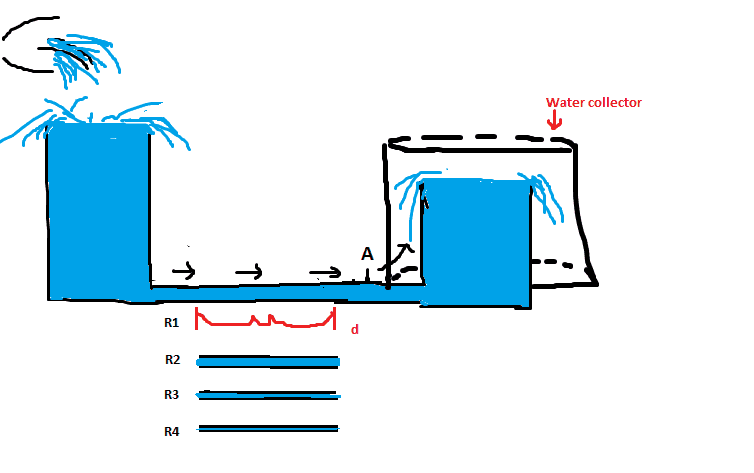There are 2 comunicating vessels. The highest vessel is coninuosly alimented with new water. Water in excess flows down on the sides.
Water will try to reach the same height in both vessels, so some water will pour out of the shortest one and will be collected by the water collector.
The pipe distance d and the point A are our elements of interest.
The pipe distance d can be considered our main resistance to the flow, and it increases as the pipe become of a smaller diameter ( R1, R2, R3, R4 ).
In the first scenario, the pipe distance d doesn't get restricted so the pressure at point A should be the pressure exerted by the left vessel's water column minus the pressure exerted by the right vessel's water column.
Flow should be from left to right since the right vessel is higher, shouldn't?
What does it happen if we restrict the pipe distance d, given that some water is always able to flow through it ( Resistance it's not infinity )?
If we restrict the pipe distance d shouldn't pressure exerted by the water coming from the restricetd pipe too weak respect at point A to overcome the presssure exerted by the right vessel's water column?
If this is correct, shouldn't flow stop,or reverse and then stop?

 

[DrClaude]

If we restrict the pipe distance d shouldn't pressure exerted by the water coming from the restricetd pipe too weak respect at point A to overcome the presssure exerted by the right vessel's water column?

What is important is the difference in pressure form the left and the right.

 

[jbriggs444]

Increasing resistance reduces the flow rate at a given pressure differential. In order to reduce the flow rate to zero you would need an infinite resistance.

 

[jrmichler]

A friend learned the hard way that water flows downhill regardless of the length of the pipe. It was a setup similar to your sketch. The pipe was 4800 feet of 2 inch PVC, and the elevation difference 10 feet. The liquid was chlorine dioxide in water solution. There was a pump on the supply tank, and several flow control valves on the discharge end. After the first startup test, he shut the pump off, and left. The flow control valves, in a different building, went full open. Part of the paper mill had to be evacuated until a valve was closed and the vapors cleared out. But he learned that water flows downhill, even through long pipes.

The math for this situation is shown in a Moody chart. The math still works for long, small diameter pipes with low pressure differences. The Reynolds number just gets smaller. A very large pipe would be analyzed using the Bernoulli equation.

 

[Chestermiller]

In the first scenario, the pipe distance d doesn't get restricted so the pressure at point A should be the pressure exerted by the left vessel's water column minus the pressure exerted by the right vessel's water column.

On what basis have you made this statement. It makes no sense to me.