Work done by gravity and by a spring

[EmmanuelE]

Homework Statement

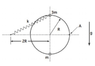
I have two objects that slide without friction on a circle of radius R, oriented in a
vertical plane, as seen on the attached photo.

The heavier object (mass = 3m) is attached to a spring with an unstretched length of zero and spring constant k. The fixed end of the spring is then attached to a point a horizontal distance 2R from the center of the circle. It is stated that the lighter object (mass = m) is initially at rest at the bottom of the ring, and that the heavier object is released from rest at the top of the ring. Then it collides with and sticks to the lighter object.

I need to answer the following questons:
What is the work done by gravity and the work done by the spring on the masses (mass=4m) from the release of the heavy particle until they both stop at point A in the figure?

Homework Equations

I found the kinetic energy of the heavy particle in the left of the ring to be:
Kleft = 3∙m∙g∙R + 2kR

The Attempt at a Solution

So far, I have determined potential energy for the heavy particle in the highest and the point mostly to the left. In the highest point, the kinetic energy is 0, but the potential energy is not zero, since it has both gravitational (mgh) and the elastic energy. I found the gravitational potential energy to be U_h = Mgh = 3mg2R and the spring energy to be: U_k = 1/2 kx² where x is the length of the spring and k is the elastic constant.

I then determined the total potential energy:
U = U_k + U_h = 6mgR + 5/2 kR

When we look at the left position instead we can only know potential energy, since U_h = 3mgR this time and U_k = 1/2 kR. For us to find the potential energy we need to use the conservation of energy. The energy the particle had at the start is conserved, and therefore we have:
K+U (start) = K+U (left),

K_start = 0, since the particle is at rest, so we find that:
K_left = U_start - U_left = (6mgR + 5/2 kR) - (3mgR + 1/2 kR) = 3mgR + 2kR

I have also been able to find the value m that will allow the combined object to just reach point A and not go any further/higher. I found the value for m to be:
m = (4kR) / g

I assume that I can use this information to be able to find the work done by gravity in this point, where they both stop.

 

[TSny]

Hello and welcome to PF!

You do not need to use conservation of energy to find the work done by gravity and the spring.

These are conservative forces. How is the work done by a conservative force related to the potential energy associated with the force?

 

[EmmanuelE]

Hello and welcome to PF!

You do not need to use conservation of energy to find the work done by gravity and the spring.

These are conservative forces. How is the work done by a conservative force related to the potential energy associated with the force?

The work done by gravity on the particles must be dependent only on the height, since it is a conservative force. If that is the case, then the work done by gravity on the object must be equal to the change in potential energy? Now as for the spring...

 

[TSny]

the work done by gravity on the object must be equal to the change in potential energy?

Almost. The work done by a conservative force is equal to the negative of the change in potential energy.

Now as for the spring...

Same.

 

[EmmanuelE]

Almost. The work done by a conservative force is equal to the negative of the change in potential energy.

Same.

Based on your answer, I have the following reasoning on how to solve the problem.

A the top where the heavy particle starts, its kinetic energy must be zero, since it is stated that the heavy particle is at rest. Therefore, we have K = 0. At this position, the potential energy is not zero, so we need to decode which elements contribute to the potential energy. The potential energy both has gravitational and elastic energy associated with it.

I decide to lay my coordinate system, so the zero of gravitational energy is where m is on the photo. Then the potential energy due to gravity for 3m must be:
U_h = mgh = 3*m*g*2*R = 6mgR

As for the spring energy, we must have:
U_k = 1/2 * k * x^2 , where k is the elastic constant and x is the length of the spring.

I need to find another way to express x^2 to replace it in the equation above, so we have:
x = sqrt((4R^2 + R^2)) = sqrt(5) * R

Therefore, we can write the spring energy as:
U_k = 5/2 kR

Now the total potential energy must be the sum of the potential energy due to gravity and the spring energy, and therefore we have:
U = U_k + U_h = 6mgR + 5/2 kR

This must be the total potential energy, now how do I use that to calculate the (negative) change in potential energy due to gravity and the spring?

 

[TSny]

Therefore, we can write the spring energy as:
U_k = 5/2 kR

A little slip here. Note that this expression does not have the correct dimensions for potential energy.

Now the total potential energy must be the sum of the potential energy due to gravity and the spring energy, and therefore we have:
U = U_k + U_h = 6mgR + 5/2 kR

This must be the total potential energy

Yes, that's the total initial potential energy of the system.

now how do I use that to calculate the (negative) change in potential energy due to gravity and the spring?

Can you repeat what you did for the initial potential energy in order to get the final potential energy at point A?

 

[EmmanuelE]

Can you repeat what you did for the initial potential energy in order to get the final potential energy at point A?

I started with the kinetic energy at the highest point. The particle is at rest, so K = 0. Then I wanted to determine the potential energy. It has both a gravitational (mgh) and elastic energy that together make up the total potential energy.

I then wanted to determine the potential energy due to gravity for the heavy particle with a mass of 3m:
U_h = mgh = 3 *m*g*2*R = 6*m*g*R

And the spring energy:
U_k = 1/2 * k * x^2 = 1/2 * k * ( sqrt ((4R^2 + R^2) ) = 1/2 * k * sqrt(5) *R = 1/2 * sqrt(5) * k * R = sqrt(5)/2 * k * R

* k is the elastic constant
* x is the length of the spring
* R is the radius of the circle

Since the initial potential energy is the sum of the potential energy due to gravity and due to the elastic energy, it must be:
U = U_k + U_h = 6mgR + sqrt(5)/2 * k*R

Which is equal to the final potential energy at point A.

 

[TSny]

I then wanted to determine the potential energy due to gravity for the heavy particle with a mass of 3m:
U_h = mgh = 3 *m*g*2*R = 6*m*g*R

OK

And the spring energy:
U_k = 1/2 * k * x^2 = 1/2 * k * ( sqrt ((4R^2 + R^2) ) = 1/2 * k * sqrt(5) *R = 1/2 * sqrt(5) * k * R = sqrt(5)/2 * k * R

Did you forget to square the expression for x?

The initial KE of the system is zero and the final KE of the system is zero. But you cannot conclude from this that the overall change in PE is zero. That would be true if mechanical energy is conserved between initial and final points. What type of collision takes place at the bottom: elastic or inelastic?

I interpret the problem as asking for the work done by gravity alone and also by the spring alone. You can then add them to get the total work done by both gravity and the spring.

 

[EmmanuelE]

OK
The initial KE of the system is zero and the final KE of the system is zero. But you cannot conclude from this that the overall change in PE is zero. That would be true if mechanical energy is conserved between initial and final points. What type of collision takes place at the bottom: elastic or inelastic?

I interpret the problem as asking for the work done by gravity alone and also by the spring alone. You can then add them to get the total work done by both gravity and the spring.

I believe your interpreting is right, so I will handle the work done by gravity and by the spring separately:
U_h = mgh = 6*m*g*R

U_k = 1/2 * k * x^2 = (5kR) / 2

Now I need to find the potential energy in point A, for gravity and the spring separately and then use that to find the change in potential energy? I believe that is the way to solve the problem, but I do not see how we do it.

 

[haruspex]

U_h = mgh = 6*m*g*R

That is the work done by gravity from the initial position to when the masses collide. You are asked for the net work done gravity from the initial position to when both masses are at point A.

U_k = 1/2 * k * x^2 = (5kR) / 2

You have a distance-squared term on the left but not on the right.
Changing the R to R² fixes that, but the coefficient is wrong. That would be the total initial energy stored in the spring. At no point is all of that released.

 

[EmmanuelE]

That is the work done by gravity from the initial position to when the masses collide. You are asked for the net work done gravity from the initial position to when both masses are at point A.

You have a distance-squared term on the left but not on the right.
Changing the R to R² fixes that, but the coefficient is wrong. That would be the total initial energy stored in the spring. At no point is all of that released.

So what would be my method for finding the work done by the spring? As you say, now I have the total initial energy stored in the spring, but all of it is not released.

 

[TSny]

Find an expression for the potential energy of the spring when the masses are at point A.