BlasterV
- 38
- 0
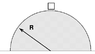
A perfect hemisphere of frictionless ice has radius R = 8 meters. Sitting on the top of the ice, motionless, is a box of mass m = 10 kg.
The box starts to slide to the right, down the sloping surface of the ice. After it has moved by an angle 14 degrees from the top, how much work has gravity done on the box?
Ok I did W = Arc length * Gravitation force
W = ((14 / 360)2PI*8m )( 9.8 m/s^2 * 10 kg )
Can someone tell me what I'm doing wrong here? Thanks. I have attached a GIF
How fast is the box moving?
Once part one is right, this is easy, since W = 10kgV^2. The problem is finding part one.
The box starts to slide to the right, down the sloping surface of the ice. After it has moved by an angle 14 degrees from the top, how much work has gravity done on the box?
Ok I did W = Arc length * Gravitation force
W = ((14 / 360)2PI*8m )( 9.8 m/s^2 * 10 kg )
Can someone tell me what I'm doing wrong here? Thanks. I have attached a GIF
How fast is the box moving?
Once part one is right, this is easy, since W = 10kgV^2. The problem is finding part one.