1/2"
- 98
- 0
Homework Statement
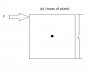
In the figure shown a square plate of mass M and side of length L
is fixed at the center . The force F makes the square plate rotate.
The force is always perpendicular to the side.
Find the work done by the force.
Homework Equations
Work = torque x θ
The Attempt at a Solution
I considered the moment arm to be half of the diagonal of length L/√2
Then the force acting perpendicular to it will be F/√2
Torque =FL /2 but then how do i find the angle covered?
The book's answer is (3F2t2)/M
Attachments
Last edited: