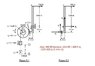
The discussion revolves around calculating gravitational energy and kinetic energy in a rotational motion problem. Participants express confusion about determining the correct radius to use for calculations, debating whether to use the axle or wheel radius. The importance of maintaining a consistent datum point for gravitational potential energy calculations is emphasized, with clarification that the gravitational potential energy is zero at the datum. The conversation also highlights the distinction between linear and rotational work, noting that work can be expressed in terms of force times distance or torque times angle, but not both simultaneously for the same force. Ultimately, participants work through the equations to arrive at the correct expressions for energy and work in the context of the problem.