SLTH02
- 5
- 1
- Homework Statement
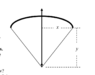
- A ballista is essentially a very large bow and arrow, except that it fires 3-m long, 2-kg arrows. The arrows are propelled by the stretched bowstring and bow, which behave as if they are two nonlinear springs that each behave according to the equation
F = -kx1.5, where the force constant k = 500 N·m-1.5 and equilibrium length l = 0.5 m. The ballista is cocked, so that the distances x and y are 1.0 m and 1.3 m, respectively. A constant 10-N frictional force opposes all motion of the arrow. The arrow is shot straight upwards. As the arrow moves upward, the distance y changes but the distance x does not.
The answer is suppose to be 70.7 J
- Relevant Equations
- WK = Fdcos(x)
Work done by non conservative force = change in mechanical energy
E final = (1/2)(500)(1.14012)^2 = 324.968 J
E initial = (1/2)(500)(0.5)^2 = 62.5 J
E final - E initial = 262.468 J
E initial = (1/2)(500)(0.5)^2 = 62.5 J
E final - E initial = 262.468 J