Jac8897
- 25
- 0
Write the expression for the infinitesimal radial inertal force dfr "look at pic"
Consider the non-uniform rigid disc of Figure 1. The density of the material is variable and depends
on the radial position: p = p (r). Its analytical expression is
p=po+p(1)
and where Po and P(1) are known and constants. Note that the density changes only with the radial coordinate:
for a given r changing θ does not affect the density. It should he observed that equation 1 implies that at
the center of the disk (r = O) the density presents its minimum value (p = Po) and for r = R the density
reaches the maximum value (p = po + P1 R)
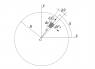
The radius of the disc is R and its uniform thickness is h. The generalized coordinate is represented by
the angle θ (see Figure 1). The disc can only rotate with respect to G and the translation is not allowed. The
effects of the gravitational forces are not considered (the disc is supposed to rotate in a horizontal plane).
The angular acceleration dθ and the angular velocity d^2θ are supposed to be non-zero quantities. The generic infinitesimal element of disc is identified by the radial coordinate r (note that 0<r< R) and angular
position θ (note that O<θ< 2∏). The infinitesimal element of disc has mass dm and is subjected to the
infinitesimal radial inertial force dFr and the infinitesimal tangential inertial force dFθ
f=ma
f=ma >>> df(r)=dm*a(r)
a(r)= r"-r(θ')^2
dm=dr*dθ*h*d(rho)
∴ dfr=(-r(θ')^2)(dm)
is this correct based on the question, my English is not so good so I am not sure if i am answering what the problem is asking.
Also on the dm part I understand that infinitesimal is just a tiny piece of the disk so to find the mass i would need a change in radius a change in angle since the high states constant i leave h but since the mass changes i do d(rho)/dr since it changes with the radius but if i put it in my dm equation i would get something like this
dm=dr*dθ*h*d(rho)/dr >>>> dm=dθ*h*d(rho) ? is this right?
Consider the non-uniform rigid disc of Figure 1. The density of the material is variable and depends
on the radial position: p = p (r). Its analytical expression is
p=po+p(1)
and where Po and P(1) are known and constants. Note that the density changes only with the radial coordinate:
for a given r changing θ does not affect the density. It should he observed that equation 1 implies that at
the center of the disk (r = O) the density presents its minimum value (p = Po) and for r = R the density
reaches the maximum value (p = po + P1 R)
The radius of the disc is R and its uniform thickness is h. The generalized coordinate is represented by
the angle θ (see Figure 1). The disc can only rotate with respect to G and the translation is not allowed. The
effects of the gravitational forces are not considered (the disc is supposed to rotate in a horizontal plane).
The angular acceleration dθ and the angular velocity d^2θ are supposed to be non-zero quantities. The generic infinitesimal element of disc is identified by the radial coordinate r (note that 0<r< R) and angular
position θ (note that O<θ< 2∏). The infinitesimal element of disc has mass dm and is subjected to the
infinitesimal radial inertial force dFr and the infinitesimal tangential inertial force dFθ
Homework Equations
f=ma
The Attempt at a Solution
f=ma >>> df(r)=dm*a(r)
a(r)= r"-r(θ')^2
dm=dr*dθ*h*d(rho)
∴ dfr=(-r(θ')^2)(dm)
is this correct based on the question, my English is not so good so I am not sure if i am answering what the problem is asking.
Also on the dm part I understand that infinitesimal is just a tiny piece of the disk so to find the mass i would need a change in radius a change in angle since the high states constant i leave h but since the mass changes i do d(rho)/dr since it changes with the radius but if i put it in my dm equation i would get something like this
dm=dr*dθ*h*d(rho)/dr >>>> dm=dθ*h*d(rho) ? is this right?
Attachments
Last edited: