Writing a recursive definition of the set permutation function

[W3bbo]

(Apologies for the lack of LaTeX formatting - I usually do my typesetting with MathType, but I only have Microsoft Equation Editor on this computer which doesn't have LaTeX export).

This isn't a homework question, but is problem I've discovered I'm facing after diving into another problem, but I digress:

Consider this set, A:

A = { T, T, R }

It has six proper permutations, but only three distinct permutations:

TTR, TRT, RTT

The expression for the number of unique permutations (in this case) is:

|A|! / ( |'T' elements| ! * |'R' elements| ! )

So: 3! / 2! * 1! which is 6/2 == 3

Due to certain requirements, I need to express this function recursively. Because the factorial function is used, I figured I could take it from there.

The expressions below take the permutation-count formula and assumes that every set A is comprised of N 'T' elements, and M 'R' elements and is called "routes".

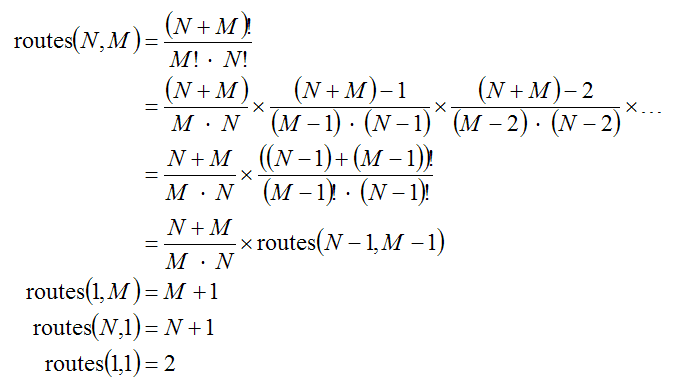
...but I can't figure out how to make it recursive. Note the huge error on the third line down, it does not follow from the line above.

Is a recursive definition even possible?

Thanks!

 

[Edgardo]

You can express a binomial coefficient recursively like this (see wikipedia article):
$$\begin{pmatrix} n \\ k \end{pmatrix} = \begin{pmatrix} n-1 \\ k-1 \end{pmatrix} + \begin{pmatrix} n-1 \\ k \end{pmatrix}$$

You can interpret this as Pascal's triangle.