Miike012
- 1,009
- 0
Homework Statement
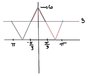
I have to fill in the missing info...
Y=A*Sin[B(x-c)] +D
A = 3. For finding the amplitude all I have to do it multiply 1/2 by the range?
D = 3. For finding upward shift all I have to do is see if the center has moved up?
period = 4pi/3 so B = 3/2
I am confused on how to find the phase shift... can I implement a,b, and d into my equation and solve for C somehow?
By just looking at the picture is looks like c could eaither be + or - pi/3 ?
But I would like to solve for this algebraically.