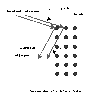X-Ray Diffraction Homework: Find Lattice Spacing d

[ShotgunMatador]

Homework Statement

X-rays of wavelength λ are incident on a cubic crystal with spacing d as shown in the figure. The incident angle is fixed at θ_i degrees. A detector is rotated from perpendicular to the 100 plane (90 degrees (grazing)) until the first maximum is detected at θ_s degrees due to interference from the 100 plane. What is the lattice spacing, d, of the cubic crystal?

Homework Equations

Bragg's Law : mλ=2dsinθ

The Attempt at a Solution

Known: m=1, λ
The angle to be used for Bragg's Law is not the incident/reflected angle because θ_s does not equal θ_i. So I figured out the angle between the incoming and reflected ray (180-θ_s-θ_i=θ_split) and that would not be the angle we are looking for either. So i divided that θ_split by 2, and subtracted it from 90. To find what I thought was the correct angle but apparently not.

If this is not the angle, what is and how do i get to it?
Is m≠1 despite the problem stating "first order maximum"?
is my θ_s not the correct angle?

Thank you in advance. also sorry about the images, they work better if you drag them into a new tab.

 

[Charles Link]

This is not (IMO) characteristic of what are typically called Bragg maxima, which need to meet two conditions : 1) The angle of incidence equals angle of reflection, and 2) The reflected rays(waves) from adjacent planes must constructively interfere. Here, the first condition is not met. (You will get a peak, and it could perhaps even be called a Bragg peak, but it is not the extremely intense type of Bragg peak that you get when conditions (1) and (2) are both met). $\\$ For this one, simple interference principles and equations will apply (and get you the answer) with a slight modification. The simple interference/diffraction equations usually are written with zero degree angle of incidence and you get $m \lambda=d \sin(\theta_s)$ for the interference maxima. $\\$ Question for you (I am not allowed to give you the answer, at least not without some effort on your part) How would the interference equation be modified for a bunch of equally spaced slits if the incident angle were $\theta_i$ instead of zero degrees? For a couple hints on this, at normal incidence, ( $\theta_i=0$), why is the path distance difference between adjacent slits (or scatterers) equal to $d \sin(\theta_s)$ ? What is the additional path distance difference (between rays at adjacent slits) that occurs if the incident angle is some non-zero $\theta_i$? How would you then get the total path distance difference between rays from adjacent slits(or scatterers) in the case of a non-zero $\theta_i$ plus a $\theta_s$, and what is the condition for constructive interference between the rays from adjacent slits (or scatterers)? How does your modified equation for constructive interference read for this (more general non-zero $\theta_i$) case? From this equation you can compute the distance $d$ between the crystal planes.