Franco
- 12
- 0
Hello again,
I don't understand how to derive equations.
#1
C = YI / r
Y = Young's modulus of the material
r = radius of curvature of the neutral surface
I = geometrical moment of inertia of the cross section of the beam
C = bending moment
#2
I = wt^3 / 12
I = moment of inertia
w = width of rectangular beam
t = thickness of rectangular beam
#3
Koenig's Apparatus
theta = h / 2(d+2D)
theta =angle of deflection
d = distance between mirrors on rectangular beam
D = distance between mirror(mirror which is closer to telescope) to scale
h = difference between the reading of scale
Thank you :D
i'm not good wif deriving equations :(
oh, and one more
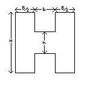
have a question asking me to arrange three beams in the order of their radius of curvature when Y, C and A are equal, the three beams are Round beam, Square beam, H-shaped beam.
i just need to find equations for moment of inertia for these shapes?
I don't understand how to derive equations.
#1
C = YI / r
Y = Young's modulus of the material
r = radius of curvature of the neutral surface
I = geometrical moment of inertia of the cross section of the beam
C = bending moment
#2
I = wt^3 / 12
I = moment of inertia
w = width of rectangular beam
t = thickness of rectangular beam
#3
Koenig's Apparatus
theta = h / 2(d+2D)
theta =angle of deflection
d = distance between mirrors on rectangular beam
D = distance between mirror(mirror which is closer to telescope) to scale
h = difference between the reading of scale
Thank you :D
i'm not good wif deriving equations :(
oh, and one more
have a question asking me to arrange three beams in the order of their radius of curvature when Y, C and A are equal, the three beams are Round beam, Square beam, H-shaped beam.
i just need to find equations for moment of inertia for these shapes?