Remi David
- 2
- 1
Hello !
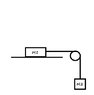
Two blocks M1 and M2 are connected by a string of negligible mass. If the system is released from rest, find how far block M1 slide in time ##t##. Neglect friction.
Diagram:
See Attached Image
Clue given in the manual:
If M1 = M2, then solution is ##x(t)= \frac{gt^2}{4}##
[/B]
Newton's Laws:
##\sum_{}^{} \vec{F} = m\vec{a}##
## \vec{F}_{m1/m2} = -\vec{F}_{m2/m1} ##
Relation between ##x(t)##, ##\vec{v}(t)##, ##\vec{a}(t)##:
##\vec{v}(t) = \frac{dx}{dt}##
##\vec{a}(t) = \frac{dv}{dt}##
So I started the exercise by separating the two masses M1 and M2, and I did a diagram with all the forces exerting on each masses.
Then I used my two Newton's laws, to find out the relation between:
1) The tension generated on each masses (Newton third law)
2) Acceleration of M2 based on the tension generated by M2
Here is my approach:
I wrote down:
##\sum_{}^{} \vec{F}_{M2} = m_{M2}\vec{a}_{M2}##
##\sum_{}^{} \vec{F}_{M1} = m_{M1}\vec{a}_{M1}##
So, with ##\vec{T}## being the tension applied to the string, and ##\vec{R}## the resistance from the table:
##\vec{T}_{M2} - \vec{W}_{M2} = m_{M2}\vec{a}_{M2}##
##\vec{R}_{M1} - \vec{W}_{M1} + \vec{T}_{M1} = m_{M1}\vec{a}_{M1}##
I simplified the equation for M1, by suppressing ##\vec{R}_{M1}## and ##\vec{W}_{M1}## as ##\vec{R}_{M1} - \vec{W}_{M1} = 0##
I concluded that tension generated by M2 was the tension applied on M1
So,
##\vec{T}_{M2} = - \vec{T}_{M1}##
##\vec{T}_{M1} = - m_{M2}\vec{g}##
using that relation, we can write:
## \vec{a}_{M1} = \frac{m_{M2}}{m{_M1}}g##
Differentiating , I found that:
##\vec{v}(t) = v_{0} + \frac{m_{M2}}{m{_M1}}gt ## with ## v_{0} = 0##
##\vec{x}(t) = x_{0} + \frac{m_{M2}}{2m{_M1}}gt^2 ## with ## x_{0} = 0##
As per the clue given in the manual, I should have a "4" instead of a "2" on the last equation... Looks like my mistake is coming for my differentiation, but I have no idea why... The "4" will come when differentiating a ##x^3##.
Don't give me the answer, I just want to have clues as I'm looking to improve (I'm not involved in any kind of scholarship at this time, and I'm doing that for my personal pleasure :D).
Sorry if my English is not the best, English is not my first language (but I'm trying to improve as well)
Thanks
Have a good day
Rémi
Homework Statement
Two blocks M1 and M2 are connected by a string of negligible mass. If the system is released from rest, find how far block M1 slide in time ##t##. Neglect friction.
Diagram:
See Attached Image
Clue given in the manual:
If M1 = M2, then solution is ##x(t)= \frac{gt^2}{4}##
Homework Equations
[/B]
Newton's Laws:
##\sum_{}^{} \vec{F} = m\vec{a}##
## \vec{F}_{m1/m2} = -\vec{F}_{m2/m1} ##
Relation between ##x(t)##, ##\vec{v}(t)##, ##\vec{a}(t)##:
##\vec{v}(t) = \frac{dx}{dt}##
##\vec{a}(t) = \frac{dv}{dt}##
The Attempt at a Solution
So I started the exercise by separating the two masses M1 and M2, and I did a diagram with all the forces exerting on each masses.
Then I used my two Newton's laws, to find out the relation between:
1) The tension generated on each masses (Newton third law)
2) Acceleration of M2 based on the tension generated by M2
Here is my approach:
I wrote down:
##\sum_{}^{} \vec{F}_{M2} = m_{M2}\vec{a}_{M2}##
##\sum_{}^{} \vec{F}_{M1} = m_{M1}\vec{a}_{M1}##
So, with ##\vec{T}## being the tension applied to the string, and ##\vec{R}## the resistance from the table:
##\vec{T}_{M2} - \vec{W}_{M2} = m_{M2}\vec{a}_{M2}##
##\vec{R}_{M1} - \vec{W}_{M1} + \vec{T}_{M1} = m_{M1}\vec{a}_{M1}##
I simplified the equation for M1, by suppressing ##\vec{R}_{M1}## and ##\vec{W}_{M1}## as ##\vec{R}_{M1} - \vec{W}_{M1} = 0##
I concluded that tension generated by M2 was the tension applied on M1
So,
##\vec{T}_{M2} = - \vec{T}_{M1}##
##\vec{T}_{M1} = - m_{M2}\vec{g}##
using that relation, we can write:
## \vec{a}_{M1} = \frac{m_{M2}}{m{_M1}}g##
Differentiating , I found that:
##\vec{v}(t) = v_{0} + \frac{m_{M2}}{m{_M1}}gt ## with ## v_{0} = 0##
##\vec{x}(t) = x_{0} + \frac{m_{M2}}{2m{_M1}}gt^2 ## with ## x_{0} = 0##
As per the clue given in the manual, I should have a "4" instead of a "2" on the last equation... Looks like my mistake is coming for my differentiation, but I have no idea why... The "4" will come when differentiating a ##x^3##.
Don't give me the answer, I just want to have clues as I'm looking to improve (I'm not involved in any kind of scholarship at this time, and I'm doing that for my personal pleasure :D).
Sorry if my English is not the best, English is not my first language (but I'm trying to improve as well)
Thanks
Have a good day
Rémi