Zero Force Member Help: Find P & Distinguish in Figures 10.7 & 10.12

[ahennessey]

I need some help distinguishing the zero force member on two different trusses.

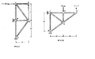
In Figure 10.7:

I said that Member CD and DE were zero force members. Is that right?

In Figure 10.12:

I said that Member AD was a zero force member? I am unsure how to find the force P as well?

The vertical deflection at C is zero with the Area for all bars = 1.8in^2 and E= 30000 KSI

Just need some help since I am a little stuck. Thanks!

 

[nvn]

ahennessey: On problem 10.7, your answer is correct. Nice work. Problem 10.12 is rather nontrivial. Your current answer is incorrect. You would need to list relevant equations and show your work, or list some of your answers, so we could see where (if) your math is incorrect.