MarcL
- 170
- 2
P.S I know I am not supposed to use attachment but there are no way for me to input the table in a clean way... same for the logic circuit drawing. Would anyone mind helping me?
1. Homework Statement
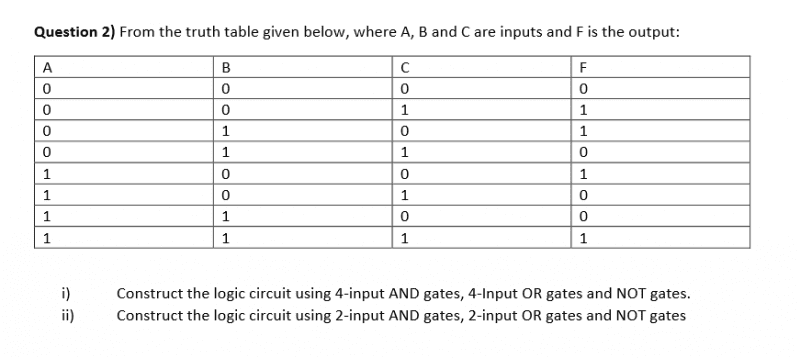
AND gates require both input to be True to get a true ouput
NOT gates are just the opposite of what you input in them ( 1 -- > 0 and 0 --> 1)
OR gates require at least one input to be true to create a true output

It just seems very... weird that there are only 4 a inputs where as in the truth table there are 8 inputs in the truth table. Anybody can help me understand that?
1. Homework Statement
Homework Equations
AND gates require both input to be True to get a true ouput
NOT gates are just the opposite of what you input in them ( 1 -- > 0 and 0 --> 1)
OR gates require at least one input to be true to create a true output
The Attempt at a Solution
I can't seem to understand why the answer key uses 4 AND gates with 3 output. Like the one below :It just seems very... weird that there are only 4 a inputs where as in the truth table there are 8 inputs in the truth table. Anybody can help me understand that?