kthejohnster
- 23
- 0
Homework Statement
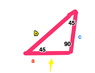
A 45,45,90 glass triangular prism (n=1.52) is surrounded by air. If a light ray comes into one of the legs (not hypotenuse) at a right angle which legs have total internal reflection?
Homework Equations
n_1sinx_i=n_2sinx_r
The Attempt at a Solution
i figured out that the light ray on the first incident leg transmits light to hypotenuse at but am getting confused on how to get the reflection angle at the hypotenuse to figure out how light hits the other leg
Edit: the light comes in at the arrow at a right angle. What happens to light at side b and c in the attached pic
Attachments
Last edited: