stunner5000pt
- 1,443
- 4
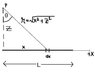
Have a look at the diagram
Find the elctric field a distance z above one end of a astraight line segment of length L which carries uniform line charge lambda. Check that your formula is consistent with what you would expect for the case z >> L
SOlution:
\lambda= q/L
dq = \lambda dx
For the electric Field in the horizontal (points to the left and is negative)
dE_{x} = \frac{1}{4 \pi \epsilon_{0}} \frac{dq}{(z^2 + x^2)} \sin \theta
Subsituting what we know about sin theta and dq
dE_{x} = \frac{1}{4 \pi \epsilon_{0}} \frac{\lambda dx}{(z^2 + x^2)} \frac{x}{\sqrt{z^2 + x^2}}
integrating x = 0 to x = L
E_{x} = \int dE_{x} = \frac{\lambda}{4 \pi \epsilon_{0}} \int_{x=0}^{x=L} \frac{xdx}{(z^2+x^2)^{\frac{3}{2}}} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{-1}{\sqrt{z^2 + x^2}} \right]_{x=0}^{x=L} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{-1}{\sqrt{z^2 + L^2}} + \frac{1}{z} \right]
E_{x} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{1}{z} -\frac{1}{\sqrt{z^2 + L^2}} \right]
ok so suppose z >> L then the electric field is zero?? Shouldnt it reduce to that of a point charge and not zero?? this should be regardless of whether i solve for x or z right??
for the Z direction i got
E_{z} = \frac{\lambda}{4 \pi \epsilon_{0}z} \frac{L}{\sqrt{L^2 + z^2}}
unlike the last one this one does reduce to the equatiopn for a point charge but is off my a factor of 1/z ...
combining the two yields
\vec{E} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{1}{z} -\frac{1}{\sqrt{z^2 + L^2}} \right] \hat{x} + \frac{\lambda}{4 \pi \epsilon_{0}z} \frac{L}{\sqrt{L^2 + z^2}} \hat{z}is there soemthing wrong with the calculationg ofr hte X Horizontal Direction?? Please help
Thank you in advance for your help and advice!
Find the elctric field a distance z above one end of a astraight line segment of length L which carries uniform line charge lambda. Check that your formula is consistent with what you would expect for the case z >> L
SOlution:
\lambda= q/L
dq = \lambda dx
For the electric Field in the horizontal (points to the left and is negative)
dE_{x} = \frac{1}{4 \pi \epsilon_{0}} \frac{dq}{(z^2 + x^2)} \sin \theta
Subsituting what we know about sin theta and dq
dE_{x} = \frac{1}{4 \pi \epsilon_{0}} \frac{\lambda dx}{(z^2 + x^2)} \frac{x}{\sqrt{z^2 + x^2}}
integrating x = 0 to x = L
E_{x} = \int dE_{x} = \frac{\lambda}{4 \pi \epsilon_{0}} \int_{x=0}^{x=L} \frac{xdx}{(z^2+x^2)^{\frac{3}{2}}} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{-1}{\sqrt{z^2 + x^2}} \right]_{x=0}^{x=L} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{-1}{\sqrt{z^2 + L^2}} + \frac{1}{z} \right]
E_{x} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{1}{z} -\frac{1}{\sqrt{z^2 + L^2}} \right]
ok so suppose z >> L then the electric field is zero?? Shouldnt it reduce to that of a point charge and not zero?? this should be regardless of whether i solve for x or z right??
for the Z direction i got
E_{z} = \frac{\lambda}{4 \pi \epsilon_{0}z} \frac{L}{\sqrt{L^2 + z^2}}
unlike the last one this one does reduce to the equatiopn for a point charge but is off my a factor of 1/z ...
combining the two yields
\vec{E} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{1}{z} -\frac{1}{\sqrt{z^2 + L^2}} \right] \hat{x} + \frac{\lambda}{4 \pi \epsilon_{0}z} \frac{L}{\sqrt{L^2 + z^2}} \hat{z}is there soemthing wrong with the calculationg ofr hte X Horizontal Direction?? Please help
Thank you in advance for your help and advice!
Attachments
Last edited: