metalmagik
- 130
- 0
The drawing shows three objects, with m1 = 11.5 kg and m2 = 23.5. They are connected by strings that pass over massless and frictionless pulleys. The objects move, and the coefficient of kinetic friction between the middle object and the surface of the table is 0.100.
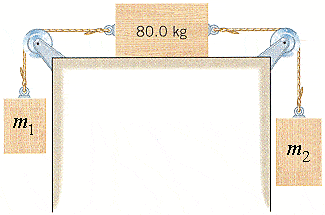
(a) What is the acceleration of the three objects?
(b) Find the tension in each of the two strings.
I made FBDs for these three blocks...and what I got ended up being the acceleration for the middle block, which came out to be 1.7 m/s^2. How do I find the acceleration of ALL three objects?? Any help is greatly appreciated, this is for a webassign and I would really like to get this correct.
(a) What is the acceleration of the three objects?
(b) Find the tension in each of the two strings.
I made FBDs for these three blocks...and what I got ended up being the acceleration for the middle block, which came out to be 1.7 m/s^2. How do I find the acceleration of ALL three objects?? Any help is greatly appreciated, this is for a webassign and I would really like to get this correct.