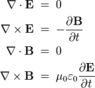Maxwell's equations VS. Lorentz & Coulomb force equations

[varga]

I find Maxwell's equations insufficient and superfluous having the Lorentz & Coulomb's force equations. As far as I see magnetic (Lorentz force) and electric (Coulomb's force) interaction is best defined by these two equations themselves, and although Maxwell's equations can describe quite a few electromagnetic interactions, by not having Lorentz force incorporated in any equation nor included as separate one, Maxwell's equations are automatically doomed to fail to describe any interaction due to this very, very important force. Did I miss something?

Why describe electric interaction with any other but with 'Electric force' equation?

Why describe magnetic interaction with any other but with 'Magnetic force' equation?*** Electric interaction
Step 1: Electric field potential given by Coulomb's law
Step 2: Electric force (acceleration vector) given by Coulomb's law

*** Magnetic interaction
Step 3: Magnetic field potential given by Biot-Savart law
Step 4: Magnetic force (acceleration vector) given by Lorentz force
====================================================

As far as I see that's all what is necessary to solve any em interaction, no?
1. Gauss's law
- This is obviously about Coulomb's law/electric potential, so why would this equation be "more suitable"?2. Gauss's law for magnetism
- divB = 0, what in the world? Instead of to describe magnetic potentials or force, to put here Biot-Savart law, or Lorentz force equation or Ampere's force law, they included some equation that has result already calculated in advance? No monopoles? That's as useful as stating "there is no other intelligent life in the Universe". 3. Faraday's law of induction
- Is there anything here we can not calculate with the time integral of four steps given above? How is this induction supposed to accurately describe complete interaction if it is oblivious to Lorentz force?4. Ampère's circuital law
- Is there anything here we can not calculate with the time integral of four steps given above? This is the best candidate to be saying something about Lorentz force, if it only included "Ampere's force law" too.
I suppose the explanation why these equations are in this form is because that is the most suitable for practical application and experimental setups, but still, my greatest concern is how any of that can accurately work without incorporating Lorentz force and Biot-Savart law in the same fashion as Coulomb's law and electric potential/force.

 

[Dale]

You do need all four of Maxwell's equations and the Lorentz equation. Biot-Savart is only an approximation to Maxwell.

 

[Born2bwire]

You do need all four of Maxwell's equations and the Lorentz equation. Biot-Savart is only an approximation to Maxwell.

To reiterate, practically the entirety of all classical electrodynamics is derived from Maxwell's equations and the Lorentz force. You really do not need much more than that. Practically any set of equations that you can reference are derivable from these five equations (Coulomb's Law (only valid for electrostatics), Biot-Savart (only valid for magnetostatics), Lorentz transformations (special relativity is automatically satisfied in Maxwell's equations), etc.). Still, Lorentz force is only really needed in terms of trajectory problems. Maxwell's equations already incorporate charge and current sources. Thus we do not need to go through the Lorentz force as a mediator for inducing current sources from fields for many problems.

 

[kcdodd]

You can think of maxwells equations as equations of motion for the field, and the lorentz force as EOM for the currents. If you are looking for a single equation, it is the EM lagrangian, which will get you to all the equations of motion for the field and currents.

 

[espen180]

3. Faraday's law of induction
- Is there anything here we can not calculate with the time integral of four steps given above? How is this induction supposed to accurately describe complete interaction if it is oblivious to Lorentz force?

4. Ampère's circuital law
- Is there anything here we can not calculate with the time integral of four steps given above? This is the best candidate to be saying something about Lorentz force, if it only included "Ampere's force law" too.

Electromagnetic waves? Ampere's Law and Faraday's Law together give the velocity and E/B ratio in electromagnetic waves. There are no charges or magnetic dipoles present in the wave. The electric and magnetic field sustain each other. Can you explain that using your time integral 4-step method?

The knowledge that radiowaves, infrared, visible light, x-rays and gamma rays all are the same phenomenon but with different energies, the prediction of the speed of light and probably the theory of relativity are thanks to Maxwell's equations.

 

[SpectraCat]

How are you going to get them accelerated electrons to emit EM radiation using your 4 step program above? Maxwell's equations and the Lorentz equation accurately describe *all* classical physical phenomena involving electricity and magnetism .. any proposed "substitute" would also need to do that, at the very least.

 

[varga]

Electromagnetic waves? Ampere's Law and Faraday's Law together give the velocity and E/B ratio in electromagnetic waves.

I'm glad you mentioned it. What waves? Yeah, I know how text-book description goes, but none of these equations has to do anything with any radiation, these equations are used to describe experimental setups with current carrying wires and permanent magnets, where properties are measured in amperes, volts, ohms and millimeters. How any of this has anything to do with any em WAVES? It is about fields, not waves. But if Maxwell's equations can describe photons, then Lorentz and Coulomb's force equations can too.

There are no charges or magnetic dipoles present in the wave. The electric and magnetic field sustain each other. Can you explain that using your time integral 4-step method?

Ok, tell me what experiment are you talking about, show the result given by Maxwell's equations and I will demonstrate I can do the same, or better, with the four steps above.

Electric and magnetic fields do not sustain each other. According to Coulomb's law, Lorentz force and Biot-Savart law, electric field is intrinsic property of any single electron (charge), while magnetic fields forms proportionally to velocity, there is no creation of any other fields here, there will always be electric field whose potential magnitude will be independent of everything, and the magnitude potential of the magnetic field of moving charge will vary according to velocity vector.

Magnetic field is EFFECT of charge motion, it is not the CAUSE for it, however since all moving electrons can interact with this magnetic field, what it can do is to cause electron displacement, i.e. it can cause electric CURRENT, but that does not mean it can be the CAUSE or CREATE any new electrostatic potential.

The knowledge that radiowaves, infrared, visible light, x-rays and gamma rays all are the same phenomenon but with different energies, the prediction of the speed of light and probably the theory of relativity are thanks to Maxwell's equations.

Can you point out what Maxwell's equation predicts the speed of light? And again, what Maxwell's equation says anything about any photons (em radiation)?

 

[varga]

How are you going to get them accelerated electrons to emit EM radiation using your 4 step program above?

You are not talking about synchrotron radiation again, or do you?

I really have no idea how Maxwell's equations do it, what are you referring to?

Maxwell's equations and the Lorentz equation accurately describe *all* classical physical phenomena involving electricity and magnetism .. any proposed "substitute" would also need to do that, at the very least.

I agree that together with the Lorentz force they do describe all. What I'm saying is that Lorentz force in this form "F= q(E + v x B)", where it is integrated with Coulomb's force, can do it alone. One equation VS. four, do you accept the challenge?

 

[espen180]

Can you point out what Maxwell's equation predicts the speed of light? And again, what Maxwell's equation says anything about any photons (em radiation)?

http://en.wikipedia.org/wiki/Electr...thesis_that_light_is_an_electromagnetic_wave"
Note that it skips a step. Instead of showing the final wave equations using the permeability and permittivity constants the author immediately substitutes them.

Compare with this to see that Maxwell's equations, using constants measures from electrostatics and magnetostatics, really does predict the wave nature and speed of electromagnetic waves.
http://en.wikipedia.org/wiki/Wave_equation#Introduction"

Note that this was before quantum physics and thus the model was later exanded to account for the particle nature of light.

 

[Dale]

I agree that together with the Lorentz force they do describe all. What I'm saying is that Lorentz force in this form "F= q(E + v x B)", where it is integrated with Coulomb's force, can do it alone. One equation VS. four, do you accept the challenge?

The Lorentz force and the Coulomb's force is woefully inadequate:
1) no way to calculate the magnetic field
2) no waves
3) no interaction between magnetic field and electric field
4) infinite speed of a propagating electric field

 

[varga]

The Lorentz force and the Coulomb's force is woefully inadequate:
1) no way to calculate the magnetic field
2) no waves
3) no interaction between magnetic field and electric field
4) infinite speed of a propagating electric field

1) no way to calculate the magnetic field

Step 3.

F= q(E + v x B); E here refers to Coulomb's Law, and B to Biot-Savart law, or at least I'll define it like that, so that basically unrolls to these four:

*** Electric interaction
Step 1: electric field potential given by Coulomb's law
Step 2: Electric force (acceleration vector) given by Coulomb's law

*** Magnetic interaction
Step 3: Magnetic field potential given by Biot-Savart law
Step 4: Magnetic force (acceleration vector) given by Lorentz force
====================================================

- How Maxwell's equations calculate magnetic field?


2) no waves

- I'll make them just like they did. What do you think E and B stand for in Maxwell's equations?


3) no interaction between magnetic field and electric field

- Magnetic and electric fields DO NOT interact.


4) infinite speed of a propagating electric field

- What is propagation speed of E and B fields in Maxwell's equations? What is the expression for E and B?

 

[varga]

http://en.wikipedia.org/wiki/Electr...thesis_that_light_is_an_electromagnetic_wave"
Note that it skips a step. Instead of showing the final wave equations using the permeability and permittivity constants the author immediately substitutes them.

Thanks, that's very interesting. Do you think you could explain the process or point someplace I can find answer to these questions:

- "To obtain the electromagnetic wave equation in a vacuum using the modern method, we begin with the modern 'Heaviside' form of Maxwell's equations. In a vacuum and charge free space, these equations are:

Taking the curl of the curl equations gives:

- What in the world curl of E and B fields, and even the curl-of-the-curl, is supposed to have with the speed of light? What are they trying to do here, how did anyone ever figure out they should combine curls to get any information about any speed?

- How can we talk about any velocity if we are not calculating FORCES, how can field potentials and their shape tell us anything about any velocity without calculating the FORCE and ACCELERATION first? I need to understand what and WHY they did so I can do the same thing with "my" equations.

Compare with this to see that Maxwell's equations, using constants measures from electrostatics and magnetostatics, really does predict the wave nature and speed of electromagnetic waves.

Is this it, the beginning of it? As a time integral my equations are already in similar form like this, can you help me make a 'wave equation' out of it?

 

[Matterwave]

3) no interaction between magnetic field and electric field

- Magnetic and electric fields DO NOT interact.

I'm just going to address this one point. If magnetic and electric fields don't interact, then how can you get propagation of an EM wave? In an electro-magnetic wave, the changing electric fields induce a changing magnetic field and vice-versa. That's how you get to propagate that wave out.

How would you explain all of EM radiation if you assert that electric fields and magnetic fields don't interact? I would like to know this.

 

[Born2bwire]

- How can we talk about any velocity if we are not calculating FORCES, how can field potentials and their shape tell us anything about any velocity without calculating the FORCE and ACCELERATION first? I need to understand what and WHY they did so I can do the same thing with "my" equations.

Electromagnetic waves do not need sources to propagate. There are no forces or accelerations, there are no charges or currents.

Is this it, the beginning of it? As a time integral my equations are already in similar form like this, can you help me make a 'wave equation' out of it?

We are the ones that are telling you that it will not work. Why should we attempt to work out assertions that are unanimously being detracted?

Again, you are using static equations for time-varying situations. This will not work.

 

[Dale]

1) no way to calculate the magnetic field

Step 3.

F= q(E + v x B); E here refers to Coulomb's Law, and B to Biot-Savart law,

That's fine, you can certainly use Biot-Savart to calculate a B field, but you cannot derive Biot-Savart from Coulomb and Lorentz force, so this is a third equation.

- I'll make them just like they did.

I would very much like to see that. Kindly post your derivation of the wave equation from only Coulomb, Lorentz force, and Biot-Savart.

- Magnetic and electric fields DO NOT interact.

Yes, they do. Google "induction".

- What is propagation speed of E and B fields in Maxwell's equations?

c, which agrees with experiment. Infinity does not.

 

[varga]

I'm just going to address this one point. If magnetic and electric fields don't interact, then how can you get propagation of an EM wave? In an electro-magnetic wave, the changing electric fields induce a changing magnetic field and vice-versa. That's how you get to propagate that wave out.

Photon is made of how many electric and magnetic fields, you say?

Please show me that equation where I can see how E and B interact.

How would you explain all of EM radiation if you assert that electric fields and magnetic fields don't interact? I would like to know this.

I'm using the same E and B fields as Maxwell, only I do calculations per point particle, so why do you think I would not to arrive to the same result?

Electromagnetic waves do not need sources to propagate. There are no forces or accelerations, there are no charges or currents.

- What is the relation between the speed of light and the curl of the curl of E and B field?

- Can E and B interact, do we add magnetic and electric vectors, do we superimpose them, or do electric only interact with electric and magnetic with magnetic fields?

Again, you are using static equations for time-varying situations. This will not work.

How about we take on some practical experiment and actually see what will work and what will not work?

I would very much like to see that. Kindly post your derivation of the wave equation from only Coulomb, Lorentz force, and Biot-Savart.

Me too, but without any help, I'll need time. Do you think Maxwell's equations were not derived from Coulomb's law and Biot-Savart law?

Yes, they do. Google "induction".

No, they do not. I explained 'induction' above. Please, show the equation you believe describes this interaction of E and B field.

c, which agrees with experiment. Infinity does not.

What is expression for E and B in Maxwell's equations?

You can think of maxwells equations as equations of motion for the field, and the lorentz force as EOM for the currents.

Yes, kind of like that, but the other way around.
This the whole point behind my arguments, thanks for that.


1.) Maxwell's equation are about em field potentials - Coulomb's law and Biot-Savart law, but approximated in relation to currents and charge densities.

2.) Lorentz force equation is about em fields and forces - Coulomb's law, Biot-Savart law, Coulomb and Lorentz force, but in relation to point charges, no approximations.


These two deal with the same E and B fields, all the same constants are there, all the relations, divergence, curl, flux or whatever is there. There is nothing in 1. that is not in 2, but there are things in 2. that are not in 1. Were approximations for charge densities and current potentials in Maxwell's equations derived from the point particle equations or was it the other way around?

 

[Born2bwire]

How about we take on some practical experiment and actually see what will work and what will not work?

Sure, here are two simple problems for you to work out.

1. What are the total fields produced by an electron that is moving in a circle of constant radius R and at some constant speed v? We will let v vary as we see fit. This can easily be done by assuming a constant B field applied normally to the plane of oscillation.

2. What are the total fields at some point (X, 0, 0) as a function of time produced by an electron located at the origin that starts at rest from t=-\infty to t = -0 and starts oscillating along the z-axis. The oscillations can be modeled as a harmonic oscillator of magnitude A and angular frequency \omega.

 

[espen180]

Photon is made of how many electric and magnetic fields, you say?

Using Coloumb and Lorentz, it is a poorly posed question to ask "how many" E or B fields. There is only a total E and B field which is a superposition of all of them. However, Maxwell can calculate the individual fields in the superposition. Coloumb/Lorentz cannot. In the case of a photon, you can say that there is a single E and B field which source each other.

Please show me that equation where I can see how E and B interact.

Faraday and Ampere's laws.

I'm using the same E and B fields as Maxwell, only I do calculations per point particle, so why do you think I would not to arrive to the same result?

There are no particles in the wave, hence the E field is the source of the B field and vice versa.

- What is the relation between the speed of light and the curl of the curl of E and B field?

The wave equation is a solution of Maxwell's equations. It shows that EM waves can only exist if they have speed c.

- Can E and B interact, do we add magnetic and electric vectors, do we superimpose them, or do electric only interact with electric and magnetic with magnetic fields?

I don't understand the question. E fields add together, as do B-fields. The time derivative of one field (ex. E) is related to the other (ex. B).

Me too, but without any help, I'll need time. Do you think Maxwell's equations were not derived from Coulomb's law and Biot-Savart law?

They weren't. They were derived experimentally.

No, they do not. I explained 'induction' above. Please, show the equation you believe describes this interaction of E and B field.

Faraday and Ampere, see above.

What is expression for E and B in Maxwell's equations?

E: Gauss and Faraday
B: Mag. Gauss and Ampere

1.) Maxwell's equation are about em field potentials - Coulomb's law and Biot-Savart law, but approximated in relation to currents and charge densities.

2.) Lorentz force equation is about em fields and forces - Coulomb's law, Biot-Savart law, Coulomb and Lorentz force, but in relation to point charges, no approximations.

Coloumb and Lorentz define E and B fields. Maxwell describes them and explains their sources.

 

[varga]

There is similar thread where everyone agreed about some of the main points I'm arguing here:

https://www.physicsforums.com/showthread.php?t=322126

OP:
I am trying to bridge a gap between Maxwell equations and Lorentz force. I know that they are not independent and in theory, one could be derived from the other but I cannot see that.

More physics oriented people prefer the Lorentz force because it describes the effect of B and E as a final force on the particle, which is good.


Born2bwire:
- Oh, one nice way you can derive the Lorentz force ...

marcusl:
- Maxwell's equations may be derived in the same way, starting from Coulomb's law...

atyy:
- The Lorentz force cannot be derived from Maxwell's equations.

atyy
- I was thinking that the Lorentz force law can't be derived from Maxwell's equations in the same way that charge conservation can...

samalkhaiat:
- No, it is not possible to derive Newton's 2nd law (i.e., Lorentz force) from Maxwell equations. If such cosistent derivation is possible, then Maxwell or Lorentz would have done it.
=====================


So, why can't we agree they can be derived one from the other, for a start?

 

[varga]

Sure, here are two simple problems for you to work out.

1. What are the total fields produced by an electron that is moving in a circle of constant radius R and at some constant speed v? We will let v vary as we see fit. This can easily be done by assuming a constant B field applied normally to the plane of oscillation.

2. What are the total fields at some point (X, 0, 0) as a function of time produced by an electron located at the origin that starts at rest from t=-\infty to t = -0 and starts oscillating along the z-axis. The oscillations can be modeled as a harmonic oscillator of magnitude A and angular frequency \omega.

Ok, but you are supposed to show the solution with Maxwell's equations. I really need to understand better what are these equations actually doing and we need the result so we can compare.


TEST EXAMPLE:
- Electron is moving in a line accelerating from 100m/s to 500m/s what is E and B equal to numerically when its velocity is 300m/s, and please say with few words how E and B change over time.

 

[varga]

However, Maxwell can calculate the individual fields in the superposition. Coloumb/Lorentz cannot. In the case of a photon, you can say that there is a single E and B field which source each other.

What is the value of E and B if an electron is moving at 400m/s?

Faraday and Ampere's laws.

Ok, two electrons move with the velocity of 900.000m/s next to each other in the same direction and separated by 0.05mm. What are the values of their E and B fields. What is their separation distance after 10 seconds?

E: Gauss and Faraday
B: Mag. Gauss and Ampere

E stands for 'electric field', what do you replace the variable E with?
B stands for 'magnetic field', what do you replace the variable B with?

Coloumb and Lorentz define E and B fields. Maxwell describes them and explains their sources.

"Define" and "describe" has pretty much the same meaning, except that 'define' is superior to 'describe'. But at least you know we are talking about the same fields and same properties.

 

[SpectraCat]

So, why can't we agree they can be derived one from the other, for a start?

Did you see the post in that thread that gives references for where you can find out how to derive the Maxwell equations from a relativistic treatment of Coulomb's law? Why not just check those out, since they seem to be what you are looking for.

I doubt that you will ever convince the rest of us that the Maxwell equations are "insufficient and superfluous" or whatever it was you said in your OP, and I am almost certain that you will not replace them with your treatment, whatever it is. What will most likely happen if you go through the derivation by yourself is that you will come up with precisely the same equations as Maxwell, thereby reinventing the wheel. Not that it won't be an instructive exercise worth doing ...

Also, it seems that Maxwell was aware of the Lorentz force, and included it in some form as one of his original 8 equations. The Lorentz force cannot be derived directly from Maxwell's equations alone, although it does follow after some reasonable assumptions are made (see http://arxiv.org/abs/physics/0206022) However, this certainly does not mean that Maxwell's equations can be derived from the Lorentz force, which is what you seem to be claiming.

 

[espen180]

1) What is the value of E and B if an electron is moving at 400m/s?




2) Ok, two electrons move with the velocity of 900.000m/s next to each other in the same direction and separated by 0.05mm. What are the values of their E and B fields. What is their separation distance after 10 seconds?



3)
E stands for 'electric field', what do you replace the variable E with?
B stands for 'magnetic field', what do you replace the variable B with?



4)
"Define" and "describe" has pretty much the same meaning, except that 'define' is superior to 'describe'. But at least you know we are talking about the same fields and same properties.

1) Gauss's Law gives the E-field and Ampere's Law Gives the B-field.

2) Troublesome integral, so I'm not going to bother with it. I'm guessing your argument is that Maxwell doesn't tell anything about forces, only fields. Even if this is true, the fields are defined from forces, so the argument doesn't work.

3) I don't understand the question.

4) I disagree. For example, I can define space-time curvature as the source of gravitational attraction, but I still don't know how to work with it. Einstein's equation describes space-time curvature and let's me do stuff. The same applies to E and B-fields.

 

[Dale]

Do you think Maxwell's equations were not derived from Coulomb's law and Biot-Savart law?

No. In fact, it is quite the other way around. Coulomb's law and the Biot-Savart law can be derived from Maxwell's equations in the electrostatic and magnetostatic limits respectively. Coulomb and Biot-Savart are special cases of the more general Maxwell, and it is simply not mathematically possible to start with only a special case and derive a generalization, you always have to go the other direction.

 

[varga]

No. In fact, it is quite the other way around. Coulomb's law and the Biot-Savart law can be derived from Maxwell's equations in the electrostatic and magnetostatic limits respectively. Coulomb and Biot-Savart are special cases of the more general Maxwell, and it is simply not mathematically possible to start with only a special case and derive a generalization, you always have to go the other direction.

Let me make sure I understand you correctly. Biot-Savart and Coulomb's law, equations for POINT PARTICLES, are special case of charge distributions and average current density used in Maxwell's equations? I suppose then 'amperes' is what describes general case, while individual charge and velocity is special case, and so the 'current' in a wire is general case and electric potential of a single charge given by the Coulomb's law is special case?

Why are you trying to disagree without even thinking, what is your agenda? Do you have something against Lorentz force or have you fallen in love with Maxwell's equations? I see absolutely no reason why would anyone take any sides in this argument. -- What is the full expression for the E and B terms found on the right side of Maxwell's equations?

 

[varga]

1) Gauss's Law gives the E-field and Ampere's Law Gives the B-field.

2) Troublesome integral, so I'm not going to bother with it. I'm guessing your argument is that Maxwell doesn't tell anything about forces, only fields. Even if this is true, the fields are defined from forces, so the argument doesn't work.

3) I don't understand the question.

4) I disagree. For example, I can define space-time curvature as the source of gravitational attraction, but I still don't know how to work with it. Einstein's equation describes space-time curvature and let's me do stuff. The same applies to E and B-fields.

Let me explain it very directly. Do you know how to apply Maxwell equations? I don't, and all I'm asking you to show me is how to do this, just once, so I can later do it myself, ok?



SIMPLE EXAMPLE:
- Electron moves along X-axis with constant velocity of 800m/s, solve for E and B.

I want to know what is E equal to, not the curl of E. There is a symbol B on the other side of equation and there is no 'B' on my calculator, so what is the full expression for that symbol? Basically, what is the full expression of this equation so I can apply it to this example and get the value of E field.

I want to know what is B equal to, not the curl of B. There is a symbol E on the other side of equation and there is no 'E' on my calculator, so what is the full expression for that symbol? Basically, what is the full expression of this equation so I can apply it to this example and get the value of B field?

 

[varga]

Did you see the post in that thread that gives references for where you can find out how to derive the Maxwell equations from a relativistic treatment of Coulomb's law? Why not just check those out, since they seem to be what you are looking for.

Before anything I must know what those symbols stand for, what is the full expression of those equations and all its terms, how to disassociate the curl from the magnitude - how to actually use those equations.

I doubt that you will ever convince the rest of us that the Maxwell equations are "insufficient and superfluous" or whatever it was you said in your OP, and I am almost certain that you will not replace them with your treatment, whatever it is. What will most likely happen if you go through the derivation by yourself is that you will come up with precisely the same equations as Maxwell, thereby reinventing the wheel. Not that it won't be an instructive exercise worth doing ...

Then you convince me, by solving one simple example. All I'm asking here is for explanation how to apply those equations, how to get some real numbers and analyze what do numbers mean.


Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s.

a.) Solve for B and E when its velocity is 700m/s.

b.) Describe briefly how E and B change during that time.

 

[Dale]

Let me make sure I understand you correctly. Biot-Savart and Coulomb's law, equations for POINT PARTICLES, are special case of charge distributions and average current density used in Maxwell's equations?

That is correct, but the reason that Maxwell is more general than Biot-Savart and Coulomb has nothing to do with point charges vs charge distributions. You can always add up an infinite number of infinitesimal point charges in order to make a charge distribution, and you can always use a delta function charge distribution to make a point charge.

The reason that the Maxwell equations are more general is that they can handle time varying charges and currents, while the Coulomb and Biot-Savart equations are limited to the electrostatic and magnetostatic cases respectively. The generality of Maxwell is not about the types of distributions that they start with (they are equivalent) but rather about the types of problems for which they are valid (Maxwell applies to many more).

 

[Frame Dragger]

Let me just to a quick favour for everyone in this thread. Varga (previously of another nickname) had a similar thread locked because of his theories about E&M, which he posted under QM for some odd reason.

After a couple of pages, the thread had to be locked. "Then you convince me" after a flurry of seemingly inane points and questions isn't a weird moment here... it's his thing. He simply isn't willing to explain in any kind of detail or provide sources to back up his "views".

Do with that information what you will, but having read the 2 pages of this thread from the start, I can see the pattern again.

 

[SpectraCat]

Before anything I must know what those symbols stand for, what is the full expression of those equations and all its terms, how to disassociate the curl from the magnitude - how to actually use those equations.

I agree with this 100%. The thing is, it takes most of us a considerable amount of time to learn all of that the first time we see this stuff (usually in college). There are formal courses that take (at least) a year that show folks how to use Maxwell's equations to solve problems in physics. You should expect to take a similar amount of time, and frankly, it's nothing short of staggeringly arrogant that you have declared them "insufficient and superfluous", without at least HAVING THIS MUCH TRAINING TO BEGIN WITH!

Get yourself some books and start reading, or enroll in a course if you want to learn about these things. It is unlikely that anyone will be willing to teach them to you over PF (I certainly am not). Jackson's "Classical Electrodynamics" (graduate level) is THE reference for this, but it is painful, and probably not the best place to start. Griffith's "Introduction to Electrodynamics" (undergraduate level) is much more accessible, but not as thorough. Still, it's probably enough for what you want at first. Fleisch's "A Student's Guide to Maxwell's Equations" is a nice set of training wheels to help get you through either text. Since I don't have much cause to use Maxwell's equations from day to day, I keep it handy as a quick reference guide, in case I need to quickly re-learn something basic.

Then you convince me, by solving one simple example. All I'm asking here is for explanation how to apply those equations, how to get some real numbers and analyze what do numbers mean.

Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s.

a.) Solve for B and E when its velocity is 700m/s.

b.) Describe briefly how E and B change during that time.

Why should I (or anyone) do your homework for you? If you can't solve such basic problems, then you shouldn't worry too much about whether or not we really need Maxwell's equations, or trying to derive substitutes. Learn about Maxwell's equations first, then criticize them.

 

[Dale]

Then you convince me, by solving one simple example. All I'm asking here is for explanation how to apply those equations, how to get some real numbers and analyze what do numbers mean.Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s.

a.) Solve for B and E when its velocity is 700m/s.

b.) Describe briefly how E and B change during that time.

SpectraCat is right, there is a reason that entire courses are devoted to this subject. However, the specific problem of the Maxwell's equation fields and potentials due to an arbitrarily moving point charge has been solved. The solution is called the Lienard-Wiechert potential. Here is the Wikipedia page:
http://en.wikipedia.org/wiki/Liénard–Wiechert_potential
but I prefer this page from Arizona State University because it shows the notation in more detail:
http://fermi.la.asu.edu/PHY531/larmor/index.html

As you can see the Lienard-Weichert field reduces to the Coulomb field for a stationary charge, but for moving charges they are different with a relativistic correction to the Coulomb field term and a radiation term for an accelerating charge. This difference is experimentally measurable and agrees with Maxwell and disagrees with Coulomb.

 

[Born2bwire]

SpectraCat is right, there is a reason that entire courses are devoted to this subject. However, the specific problem of the Maxwell's equation fields and potentials due to an arbitrarily moving point charge has been solved. The solution is called the Lienard-Wiechert potential. Here is the Wikipedia page:
http://en.wikipedia.org/wiki/Liénard–Wiechert_potential
but I prefer this page from Arizona State University because it shows the notation in more detail:
http://fermi.la.asu.edu/PHY531/larmor/index.html

As you can see the Lienard-Weichert field reduces to the Coulomb field for a stationary charge, but for moving charges they are different with a relativistic correction to the Coulomb field term and a radiation term for an accelerating charge. This difference is experimentally measurable and agrees with Maxwell and disagrees with Coulomb.

Oh nice. I only knew of Jackson that had the field equations for the Lienared-Wiechert potentials.

 

[PhilDSP]

By the way, Maxwell did include the equivalent of the Lorentz force law in his set of fundamental equations (he got there much earlier than Lorentz) But after Maxwell died, a committee of mostly British physicists restructured Maxwell's model and removed that and the linkage to scalar and vector potentials (as well as other things they thought muddled the simplicity of the 4 equation structure)

We know now that potential is more fundamental than EM fields (as the sole prominent objector to removing them, Lord Kelvin, suspected over a hundred years ago)

 

[varga]

I agree with this 100%. The thing is, it takes most of us a considerable amount of time to learn all of that the first time we see this stuff (usually in college). There are formal courses that take (at least) a year that show folks how to use Maxwell's equations to solve problems in physics. You should expect to take a similar amount of time, and frankly, it's nothing short of staggeringly arrogant that you have declared them "insufficient and superfluous", without at least HAVING THIS MUCH TRAINING TO BEGIN WITH!

Sorry if I was not clear, I do believe to have adequate education and knowledge of the subject, I also did check Wikipedia and Google, as I always do, and I even took my textbooks out, to confirm what I could. It is with this knowledge and understanding that I still decided to try Maxwell's equations vs Lorentz & Coulomb's law.

Get yourself some books and start reading, or enroll in a course...

Yep, I did all that, but here we are having this conversation about it and we have different opinions. I made my arguments and heard yours, now it is the time to prove the point with some numbers.

Why should I (or anyone) do your homework for you? If you can't solve such basic problems, then you shouldn't worry too much about whether or not we really need Maxwell's equations, or trying to derive substitutes. Learn about Maxwell's equations first, then criticize them.

Basic problem, ok. Why? Maybe because it would take less time to solve than to write what you did. / To prove your point. To have conversation. To find out the truth. To exchange information. To try to teach me a lesson. To have fun and learn... all these reasons as why you and me joined this forum, eh? That's why we're here, right?

 

[varga]

SpectraCat is right, there is a reason that entire courses are devoted to this subject.

Ok, but all I need is full expression of all the terms in any equation and calculator to see what result it gives with whatever arbitrary parameters, or I can use some actual experimental measurements and hence confirm the numbers and validity or accuracy of the equation. I do not need to know even any math to do that, just one example to see what is what. I can not solve this example myself because my argument is that it can not be done and that at best it will give the same result as what I get via Lorentz force equation.

However, the specific problem of the Maxwell's equation fields and potentials due to an arbitrarily moving point charge has been solved. The solution is called the Lienard-Wiechert potential. Here is the Wikipedia page:
http://en.wikipedia.org/wiki/Li%C3%A...hert_potential
but I prefer this page from Arizona State University because it shows the notation in more detail:
http://fermi.la.asu.edu/PHY531/larmor/index.html

As you can see the Lienard-Weichert field reduces to the Coulomb field for a stationary charge, but for moving charges they are different with a relativistic correction to the Coulomb field term and a radiation term for an accelerating charge.

Thank you, but that would prove my point as that is not one of the four equations that we call "Maxwell's equations". What error are we talking about anyway? The one due to limited speed of propagation of gravity and em field potentials? If so, then what that has to do with this example where there is only one charge? Even with two or more, how large would that error be with closely spaced charges if this effect is not even concern for interplanetary distances where gravity field of the Sun is supposed to "lag" eight *minutes* and yet we can not measure it? I again object to the involvement of special relativity, I'm talking about the velocity of ~700m/s, but nevertheless I'm very interested to compare actual results and see how large this error correction really is.

This difference is experimentally measurable and agrees with Maxwell and disagrees with Coulomb.

Ok, what experiments? Can you point some papers or articles? I'd like to know what is the difference in prediction, how much error there is in Coulomb's law and how error changes as the velocity increases, at what speed it really becomes measurable and important factor, stuff like that.


p.s. What is "Larmor radiation", is that the same, similar or completely different to "synchrotron radiation"?

 

[SpectraCat]

Ok, but all I need is full expression of all the terms in any equation and calculator to see what result it gives with whatever arbitrary parameters, or I can use some actual experimental measurements and hence confirm the numbers and validity or accuracy of the equation. I do not need to know even any math to do that, just one example to see what is what. I can not solve this example myself because my argument is that it can not be done and that at best it will give the same result as what I get via Lorentz force equation.

So let's start there .. what do you get for the Lorentz force equation?

Thank you, but that would prove my point as that is not one of the four equations that we call "Maxwell's equations".

Ummm ... no. Maxwell's equations are *general* ... this is the solution for a specific case, which is directly relevant to your question. The E & B fields are *derived from* the charge density and current density *using* Maxwell's equations. The Lienard-Weichert potentials are the *inputs* to the Maxwell's equations to allow you to calculate the fields.

What error are we talking about anyway? The one due to limited speed of propagation of gravity and em field potentials? If so, then what that has to do with this example where there is only one charge? Even with two or more, how large would that error be with closely spaced charges if this effect is not even concern for interplanetary distances where gravity field of the Sun is supposed to "lag" eight *minutes* and yet we can not measure it? I again object to the involvement of special relativity, I'm talking about the velocity of ~700m/s, but nevertheless I'm very interested to compare actual results and see how large this error correction really is.

No, read it again .. there are two corrections, one for the relativistic effects to the Coulomb field, and the other for *emission of radiation* ... you know, that phenomenon that you didn't think existed for accelerated charges? Note how the Maxwell's equations derive the existence of such a phenomenon (radiating EM waves) from the basic, simple inputs, in a manner that is consistent with experiment. That is a nice example of why the rest of us do not find them "insufficient" or "superfluous".

 

[Dale]

Thank you, but that would prove my point as that is not one of the four equations that we call "Maxwell's equations".

Yes, it is. The Lienard Weichert potentials are derived directly from Maxwells equations for the special case of a point charge (as I said earlier, a delta-function) distribution as you requested. The derivation is pretty simple and straightforward, anyone can verify it for themselves. Simply substitute in q \, \delta(\mathbf{r}-\mathbf{r0}(t)) for the charge distribution and q \, \mathbf{r0'}(t) \, \delta(\mathbf{r}-\mathbf{r0}(t)) for the current distribution and simplify.

What error are we talking about anyway?

Did you even read the links in detail? Do you see how the fields reduce to the Coulomb field for a point charge at rest? The error is then the other terms which are non-zero for a moving or accelerating charge.

 

[espen180]

Sorry if I was not clear, I do believe to have adequate education and knowledge of the subject, I also did check Wikipedia and Google, as I always do, and I even took my textbooks out, to confirm what I could. It is with this knowledge and understanding that I still decided to try Maxwell's equations vs Lorentz & Coulomb's law.

Yep, I did all that, but here we are having this conversation about it and we have different opinions. I made my arguments and heard yours, now it is the time to prove the point with some numbers.

You claim to have an understanding of Maxwell's equations. If so, why are you using the differential form to do calculations on point charges? You should know to use the integral form.

 

[Frame Dragger]

I warned you folks about him...

 

[Dale]

Hi Everyone,

Can someone check this expression for me from a reputable textbook? (my introductory text didn't go this far) I believe that the Wikipedia formula is wrong:
\vec{E}(\vec{x},t) = q\left(\frac{\vec{n}-\vec{\beta}}{\gamma^2(1-\vec{\beta}\cdot\vec{n})^3R^2}\right)_{\rm{ret}} + \frac{q}{c}\left(\frac{\vec{n}\times[(\vec{n}\times\vec{\beta})\times\vec{\dot{\beta}}]}{(1-\vec{\dot{\beta}}\cdot\vec{n})^3R}\right)_{\rm{ret}}<br />

But if my memory and understanding are right then I think the correct formula is:
\vec{E}(\vec{x},t) = q\left(\frac{\vec{n}-\vec{\beta}}{\gamma^2(1-\vec{\beta}\cdot\vec{n})^3R^2}\right)_{\rm{ret}} + \frac{q}{c}\left(\frac{\vec{n}\times[(\vec{n}-\vec{\beta})\times\vec{\dot{\beta}}]}{(1-\vec{\dot{\beta}}\cdot\vec{n})^3R}\right)_{\rm{ret}}

This is an important difference since the first form results in no radiation for an accelerating point charge which is momentarily at rest.

 

[varga]

So let's start there .. what do you get for the Lorentz force equation?

Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s.

a.) Solve for E and B when its velocity is 700m/s.

b.) Describe briefly how E and B change during that time.

According to above equations...

E field: The magnitude potential and its density distribution of E field does not change during this time. Geometrically this potential is spherical and its magnitude drops off uniformly with the inverse square law. If we trace the magnitude potential around the charge with some arbitrary but constant radius it will describe a "ball" or sphere. Therefore, I can say this field actually has no rotation (curl) and that divE = 0.

B field: The magnitude potential and its density distribution of B field does change during this time proportionally to velocity. Geometrically this potential is toroidal and its magnitude drops off uniformly with the inverse square law in a plane perpendicular to velocity vector, but it decreases as this angle goes from 90 degrees to 0 when it aligns with the velocity vector and where magnetic potential is zero, directly in line behind and in front of the charge. If we trace the magnitude potential around the charge with some arbitrary but constant radius it will describe a "ball squeezed from the front and behind" (doughnut). Therefore, I can say this field does have rotation (curl) defined by the cross product and 'right-hand rule', and that divB != 0.


Your turn, what do you get from Maxwell's equations?

Ummm ... no. Maxwell's equations are *general* ... this is the solution for a specific case, which is directly relevant to your question. The E & B fields are *derived from* the charge density and current density *using* Maxwell's equations. The Lienard-Weichert potentials are the *inputs* to the Maxwell's equations to allow you to calculate the fields.

I asked 10 times what E and B terms stand for on the right hand side of those equation. Anyway, I can use those same expressions to substitute E and B in Lorentz force equation, but why would I if error is 398 places behind the decimal point?

In CLASSICAL PHYSICS, the real input for E and B terms on the right hand side of Maxwell's equations is Coulomb's law and Biot-Savart law, is it not?

No, read it again .. there are two corrections, one for the relativistic effects to the Coulomb field, and the other for *emission of radiation* ... you know, that phenomenon that you didn't think existed for accelerated charges?

No radiation, only retarded time.

Wikipedia article explicitly states no quantum effects are taken into account

Note how the Maxwell's equations derive the existence of such a phenomenon (radiating EM waves) from the basic, simple inputs, in a manner that is consistent with experiment. That is a nice example of why the rest of us do not find them "insufficient" or "superfluous".

I hear you, but I don't see anyone is able to demonstrate any of that.

 

[Born2bwire]

Hi Everyone,

Can someone check this expression for me from a reputable textbook? (my introductory text didn't go this far) I believe that the Wikipedia formula is wrong:
\vec{E}(\vec{x},t) = q\left(\frac{\vec{n}-\vec{\beta}}{\gamma^2(1-\vec{\beta}\cdot\vec{n})^3R^2}\right)_{\rm{ret}} + \frac{q}{c}\left(\frac{\vec{n}\times[(\vec{n}\times\vec{\beta})\times\vec{\dot{\beta}}]}{(1-\vec{\dot{\beta}}\cdot\vec{n})^3R}\right)_{\rm{ret}}<br />

But if my memory and understanding are right then I think the correct formula is:
\vec{E}(\vec{x},t) = q\left(\frac{\vec{n}-\vec{\beta}}{\gamma^2(1-\vec{\beta}\cdot\vec{n})^3R^2}\right)_{\rm{ret}} + \frac{q}{c}\left(\frac{\vec{n}\times[(\vec{n}-\vec{\beta})\times\vec{\dot{\beta}}]}{(1-\vec{\dot{\beta}}\cdot\vec{n})^3R}\right)_{\rm{ret}}

This is an important difference since the first form results in no radiation for an accelerating point charge which is momentarily at rest.

Yeah, your equation is correct. That must have been a recent edition because I distinctly remember being put off by the fact that the article gave the scalar and vector potentials and not the field equations.

EDIT: Did you just fix that? I went over there to correct it but when I loaded up the edit page it had the corrected equations... sneaky...

Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s.

a.) Solve for E and B when its velocity is 700m/s.

DaleSpam just gave you the equations.

\mathbf{E}(\mathbf{r},t) = \frac{q}{4 \pi \epsilon_0} \frac{R}{\left( \mathbf{R}\cdot\mathbf{u}\right)^3} \left[ (c^2-v^2\right)\mathbf{u}+\mathbf{R}\times\left(\mathbf{u}\times\mathbf{a}\right) \right]

where

\mathbf{R}= \mathbf{r}-\mathbf{w}(t_r)
\dot{\mathbf{w}}(t_r) = \mathbf{v}

the vector w gives the postion of the particle at the retarded time t_r.

Anyway, if you do know electromagnetics as you assert then you should already be more than familiar with Maxwell's Equations, synchrotron radiation, Lienard-Wiechart potentials and etc. These are all topics in undergraduate EM physics courses. There really should be nothing to discuss.

 

[varga]

Yes, it is. The Lienard Weichert potentials are derived directly from Maxwells equations for the special case of a point charge (as I said earlier, a delta-function) distribution as you requested.

That is special relativity. Why use special relativity correction? Why not use Coulomb's law and Biot-Savart law like we are supposed to in classical electromagnetism?

Why complicate the terms of INPUT, we are looking at relation between Lorentz force and Maxwell's equations, we can use the same input terms for E and B in both, that does not help us, it only complicates unnecessarily. How large do you think this error could possibly be in our simple example?

And if Liénard-Wiechert potentials define E and B only as an INPUT for the right hand side of Maxwell's equations, then what does that mean? The values of E and B given by Liénard-Wiechert potentials are not "complete", so they need to be further processed?

Did you even read the links in detail? Do you see how the fields reduce to the Coulomb field for a point charge at rest? The error is then the other terms which are non-zero for a moving or accelerating charge.

You cut off the rest of that paragraph where I explained what I mean. "Retarded time" is an effect related primarily to DISTANCE between TWO interacting fields, the greater the distance the more "delay", more "error"...

1.) What retarded time has to do with this case and only one charge, where is the distance, distance to what? "OBSERVER"?

2.) How large do you expect error correction to be if we can not even measure the whole 8 minutes delay of Sun's gravity field?

 

[varga]

You claim to have an understanding of Maxwell's equations. If so, why are you using the differential form to do calculations on point charges? You should know to use the integral form.

My understanding may be wrong, please use whichever form suits you, and you do not need to use Special Relativity correction.

Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s. Solve for E and B when its velocity is 700m/s.

 

[varga]

Hi Everyone,
Can someone check this expression for me from a reputable textbook?
This is an important difference since the first form results in no radiation for an accelerating point charge which is momentarily at rest.

I surely would like to see numerical result of those equations applied to our example, but I still do not see how that fits back in Maxwell's equations, especially since both sets are supposed to deal with time-varying aspect of it. Are you sure those terms are input to Maxwell's equations and not something we use INSTEAD?


Now, let's stick to classical electromagnetism and go from the beginning. How are Maxwell's equations, including those E and B on the right side, defined in CLASSICAL ELECTROMAGNETISM, can you write that down please?

 

[varga]

DaleSpam just gave you the equations.

\mathbf{E}(\mathbf{r},t) = \frac{q}{4 \pi \epsilon_0} \frac{R}{\left( \mathbf{R}\cdot\mathbf{u}\right)^3} \left[ (c^2-v^2\right)\mathbf{u}+\mathbf{R}\times\left(\mathbf{u}\times\mathbf{a}\right) \right]

where

\mathbf{R}= \mathbf{r}-\mathbf{w}(t_r)
\dot{\mathbf{w}}(t_r) = \mathbf{v}

the vector w gives the postion of the particle at the retarded time t_r.

So does that gives us the full information about E field, or is that just an INPUT for the right hand side of Maxwell's equation to calculate B field? What do you think this error correction would be in our example, 534 places behind the decimal point, or larger?

Anyway, if you do know electromagnetics as you assert then you should already be more than familiar with Maxwell's Equations, synchrotron radiation, Lienard-Wiechart potentials and etc. These are all topics in undergraduate EM physics courses. There really should be nothing to discuss.

Yes, there is nothing to discuss anymore. Now it is a matter of whether any of you can actually apply these equations as you are asserting they can be applied, and you do not even need to struggle with SR and retarded time, or any corrections, just print down the damn equation that can solve this most simple example, in classical form, without relativistic corrections, like undergraduates would:

Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s.
- Solve for E and B when its velocity is 700m/s.

 

[Repainted]

I asked 10 times what E and B terms stand for on the right hand side of those equation. Anyway, I can use those same expressions to substitute E and B in Lorentz force equation, but why would I if error is 398 places behind the decimal point?

In CLASSICAL PHYSICS, the real input for E and B terms on the right hand side of Maxwell's equations is Coulomb's law and Biot-Savart law, is it not?

No. You solve Maxwell's equations to obtain an expression for the E and B.

Q: Electron accelerates along X-axis in 10 seconds from 200m/s to 900m/s.
- Solve for E and B when its velocity is 700m/s.

These were taken from the Wikipedia link that you obviously didn't read(and have been posted twice in the thread).

I think you might want to know what the the symbols mean(again from Wikipedia):

is the charges velocity divided by c and

is the vector position of the charge. The 'ret' emphasises that we are considering only the retarded solutions.
γ is the Lorentz factor and

is a unit vector pointing from the retarded position of the charge to the observer.

These were derived from Maxwell's equations, they aren't to be input into Maxwell's equations or anything. Input them into the Lorentz force law(which is basically just the definition of the E and B fields) and you get the force on a charged particle due to your moving electron.

 

[Dale]

Yeah, your equation is correct. That must have been a recent edition because I distinctly remember being put off by the fact that the article gave the scalar and vector potentials and not the field equations.

EDIT: Did you just fix that? I went over there to correct it but when I loaded up the edit page it had the corrected equations... sneaky...

Thanks for the confirmation. This is really weird. When I go to the page it displays the wrong equation, but when I go to edit it has the right equation. Do edits have to be "approved" or something before they take effect?

 

[Born2bwire]

Thanks for the confirmation. This is really weird. When I go to the page it displays the wrong equation, but when I go to edit it has the right equation. Do edits have to be "approved" or something before they take effect?

Try clearing your cache when you reload the page. I think you can do it by doing something like CTRL-F5 or refreshing several times. The page is correct when I look at it now.

 

[Dale]

That is special relativity. Why use special relativity correction? Why not use Coulomb's law and Biot-Savart law like we are supposed to in classical electromagnetism?

Because classical electromagnetism is relativistic (Maxwell's equations are Lorentz invariant). Historically, that was the whole motivation for developing special relativity. Also, as I have pointed out before, Coulomb's law simply does not apply in the situation of a moving point charge, it is an approximation to Maxwell's equations that assumes stationary charges (electrostatic).

Why complicate the terms of INPUT, we are looking at relation between Lorentz force and Maxwell's equations, we can use the same input terms for E and B in both, that does not help us, it only complicates unnecessarily.

I don't understand what you mean by "terms of INPUT". You are the one who specified a point charge. That is the only input, delta functions at an arbitrary location representing charge and current distribution due to a point charge. The Lienard-Wiechert fields are the solution of Maxwell's equations (the output result) using delta function charge and current distributions as the input representing an arbitrarily moving point charge.

I don't know how I can possibly make this any clearer. For the question you posed the answer is the Lienard-Wiechert field, which you can see is different from inappropriately applying Coulomb's law to an electrodynamic situation.

You cut off the rest of that paragraph where I explained what I mean. "Retarded time" is an effect related primarily to DISTANCE between TWO interacting fields, the greater the distance the more "delay", more "error"...

1.) What retarded time has to do with this case and only one charge, where is the distance, distance to what? "OBSERVER"?

2.) How large do you expect error correction to be if we can not even measure the whole 8 minutes delay of Sun's gravity field?

The retarded time is the distance between the source (point charge) and the position in space where you are calculating the field (divided by c). So the distance between the charge and each point in space if you are calculating the field everywhere.

I don't know what you think any of this has to do with gravity. We are talking about electromagnetism, not gravitation. It is a completely irrelevant comment. Please stick to one topic.

Now, let's stick to classical electromagnetism and go from the beginning. How are Maxwell's equations, including those E and B on the right side, defined in CLASSICAL ELECTROMAGNETISM, can you write that down please?

Did you forget how to spell google?
http://en.wikipedia.org/wiki/Maxwell's_equations#General_formulation