What I mean about "grounding a point" is that you'll later find that when people design circuits they often times have one reference point from which all other voltages are referenced, and this point is said to have 0 volts (0 is really arbitrary if you think about it because we are really just doing a potential difference, but it makes sense because you don't 5-0 is more trivially 5 than if we gave ground 1V and were subtracting one all the time; e.g. 6-1). This point is usually tied to earth, the Earth ground is kind of the ultimate reservoir of electrons, but is sometimes simply tied to chassis of a box (or is sometimes just a "signal ground" on the plane of a PCB). I didn't really want to go searching for a reference that had just the right information, so you'll have to take it from me, a lowly physicists who think he knows circuits well :p. In your circuit you can pick any point from which all other points would be referenced. Point C really makes the most sense to ground, and give zero potential.
Oh right, and the garden hose analogy. Since current is a flow, and water is a flow that's where the analogy begins. You can control the water flow by turning a spigot, analogous to voltage. Certain things, like gravel, may impede water flow just like resistors. The only thing is that I haven't really come up with an example of a water capacitor.
As for gneill's initial advice, which I was soon to echo after having read through the topic, let's address it now:
Wait a second! I agree with your i2 loop, but your i1 loop is opposite to what it should be, no? It goes from minus to plus!
As others have previously noted, you can assign whatever direction you want to your loops. If you went CCW around the right loop (indicating a CCW current) you would find out later, when you solved for the current, that you get a negative current (meaning that the actual current flow is opposite what you initially picked and really goes CW as we'd expect).
ILS, I agree that there a couple ways to solve this problem, and I fully embrace eventually tackling an alternate solution. I do, however, disagree with starting with the hardest. :p
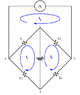
Mind if I quickly outline our a more practical approach? Also, didn't there used to be letters on your diagram?
Let's do some KVL since that's how you started. Make both loops CCW, just to demonstrate that it will work.
Right loop:
Irht*Rx+Irght*R2+Vs=0
Left loop:
Ilft*R1+Ilft*R3-Vs=0
Now for the constraint from the problem:
We know that there is no current flowing through the ammeter, which means that the leftmost point and the rightmost point are at the same potential
-Irht*R2=Ilft*R1
(you could have also used the voltage loop if what I did was confusing, going CW Irht*R2+Ilft*R1=0)
So, now there are 3 eqns and 3 unknowns, wahoo! Note: for the constraint you could also do the other voltages,
-Irht*Rx=Ilft*R3.
There's other tricks that you could use to solve this problem really quickly. If you treat the leftmost point and rightmost point as voltage dividers (look it up if you haven't seen it), you just equate them and you get the answer presto, virtually no work involved!
Sorry if I stole anyone's thunder, but the amount of complexity in this problem was getting a bit absurd, beyond being practical for learning I felt.


 , an accidental keystroke can suddenly change your keys from Latin to Hebrew and you'll spend the next hour trying to change it back.
, an accidental keystroke can suddenly change your keys from Latin to Hebrew and you'll spend the next hour trying to change it back.