robertjford80
- 388
- 0
I'm on the last chapter of a 1200 page calc book, I'm really psyched.

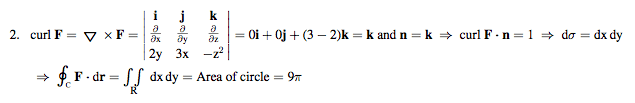
The method I learned for finding the unit normal of a vector field, n, is take the derivative of the equation and divide that by the magnitude of the derivative. This technique works for questions 3 and 4 above, but for 1,2 and 5, the solution manual just says n = k. I can't figure out why n = k. What are they talking about?
Homework Statement
The Attempt at a Solution
The method I learned for finding the unit normal of a vector field, n, is take the derivative of the equation and divide that by the magnitude of the derivative. This technique works for questions 3 and 4 above, but for 1,2 and 5, the solution manual just says n = k. I can't figure out why n = k. What are they talking about?
Last edited: